Statistical Distributions

1. 
   (a) Draw a sketch of the distribution of , indicating clearly the positions of the mean and the points of inflection.

 Solutions

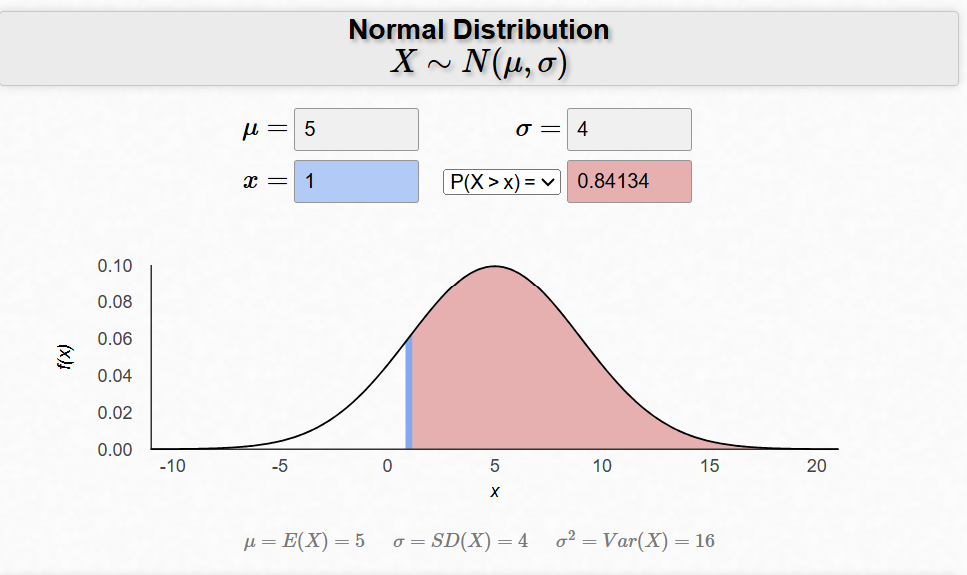
(b) Write down the value of .

 Hint

For normal distributions, the probability of a continuous random variable taking any specific value is zero.

 Solutions

To find , we first calculate . However, since is a continuous random variable, the probability of it taking any specific value is zero. Therefore, we have:

Thus,

Find .

 Solutions

To find , we first standardize the variable to convert it into a standard normal variable . The mean is 5 and the standard deviation is 4 (since the variance is 16).
Calculating the z-scores for 6 and 8:

Using standard normal distribution tables, we find the probabilities corresponding to these z-scores:

The probability is then:

2. The weights of avocados are normally distributed normally with mean 204 g and standard deviation 25 g . The avocados are classified as small, medium or large. Large avocados weigh more than 220 g , small avocados weigh less than 180 g . All other avocados are classified as medium. Calculate, to one decimal place, the percentage of avocados in each grade.

 Solutions

To find the percentage of avocados in each grade, we first calculate the z-scores for the weight limits of small and large avocados.
Calculating the z-scores:

Using standard normal distribution tables, we find the probabilities corresponding to these z-scores:

The percentage of small avocados is:

The percentage of large avocados is:

The percentage of medium avocados is:

3. Components produced by a factory machine have masses that are normally distributed.
   (a) The machine is initially set so that the mean mass is 0.249 kg and standard deviation 0.005 kg . A component is required to have a mass within the limits 0.247 kg and 0.252 kg . Calculate to the nearest whole number the percentage of components produced that are outside the required limits.

 Hint

 Solutions

To find the percentage of components outside the required limits, we first calculate the z-scores for the limits:

Using standard normal distribution tables, we find the probabilities corresponding to these z-scores:

The probability of a component being within the limits is:

Thus, the percentage of components outside the required limits is:

(b) The machine is now set so that the mean mass is , the standard deviation still being 0.005 kg . Given that of the components now have masses greater than 0.252 kg , find to 3 decimal places.

 Hint

 Solutions

To find the mean mass such that 10% of the components have masses greater than 0.252 kg, we first determine the z-score corresponding to the upper 10% of the standard normal distribution.
We want P(X > 0.252) = 0.10 for X ~ N(μ, 0.005^2). Let Z be standard normal.

Equivalently, we have

Then, Equivalently, we have

so

Hence

To three decimal places, μ = 0.246 kg.

4. A survey of 200 workers to look at their commuting time, minutes, had the following results:

(a) Calculate the mean and the standard deviation of

 Hint

 Solutions

mean minutes
Using the formula for standard deviation:

minutes

(b) It is initially assumed that can be modelled as a normal distribution.

(i) Calculate, to 3 significant figures, the probability that a commuter chosen at random has a commuting time of less than 45 minutes.

 Hint

 Solutions

Calculate the Z score for 45 minutes:

Using standard normal distribution tables, we find the probability corresponding to this Z score:

(ii) The 200 commuters are put into groups of 20. Calculate, to 2 significant figures, the probability that in a randomly selected group, fewer than 5 of them will have a commuting time of less than 45 minutes.

 Hint

 Solutions

First find the probability for a single commuter to have a commuting time of less than 45 minutes, which we calculated in part (i) as approximately 0.43.:

We will need to use the binomial distribution here.

Let Y be the number in a group of 20 with commuting time <45 minutes. Then Y∼Bin(20,p) and

Evaluating this with p≈0.4298 gives

To 2 significant figures this is 0.029 (≈2.9%).

When an additional question is asked in the survey it is found that 10 of the 200 workers have a commuting time of more than an hour and a half. Determine with a reason whether the normal distribution is suitable to model this data.

 Hint

 Solutions

To determine if the normal distribution is suitable, we can calculate the probability of a commuting time greater than 90 minutes using the normal distribution with the mean and standard deviation calculated in part (a).
Calculate the Z score for 90 minutes:

Using standard normal distribution tables, we find the probability corresponding to this Z score:

This means that approximately 24.6% of commuters are expected to have a commuting time greater than 90 minutes. However, in the survey, only 10 out of 200 workers (5%) reported a commuting time of more than an hour and a half. This significant discrepancy suggests that the normal distribution may not be suitable for modeling this data.

5. (a) The volume, litres, of a tub of one brand of paint may be assumed to be normally distributed. of the tubs contain less than 10.2 litres of paint and of tubs contain more than 10 litres of emulsion paint. Find the mean and the standard deviation to 2 decimal places.

 Hint

 Solutions

Let X ~ N(μ, σ^2). From the information:

P(X < 10.2) = 0.4 ⇒ z1 = ≈ −0.2533471031,
P(X > 10) = 0.98 ⇒ P(X ≤ 10) = 0.02 ⇒ z2 ≈ −2.0537489106.

We have

Subtracting gives

Numerically,

Then

Answers (to 2 decimal places): mean μ = 10.23 litres, standard deviation σ = 0.11 litres.

(b) The volume, litres, of a tub of another brand of paint is normally distributed with a mean of 10.15 and a standard deviation of 0.1 . A case contains 12 tubs of paint. Find, to 2 decimal places, the probability that fewer than 3 tubs contain less than 10 litres of paint.

 Hint

 Solutions

First find the single‑tub probability:

so

We need to use the binomial distribution here.

Let

Then

Evaluating the three terms:

So

To 2 decimal places the probability is 0.96.