Collecting and Interpretation Data

1. From a recent census in a particular residential area it was found that of residents had English as their main language and of the population were under 18 years old. You may assume that these characteristics are independent. The local library wants to explore this issue and decides to create a sample of 200 people.
   (a) In a stratified sample, how many of the 200 people should be 18 years old or over and have a main language that is not English?

 Hint

 Solutions

(b) Describe one difficulty of creating a stratified sample.

 Hint

 Solutions

Describe why a quota sample might be preferable to a stratified sample.

 Hint

 Solutions

2. A motoring magazine carried out a survey of the value of petrol-driven cars that were five years old. In the survey, the value of each car was expressed as a percentage of its value when new. The results of the survey are summarised in the following table and histogram.

Percentage of original value	Number of cars
	4
	12
	18
	13
	6
	5
	2

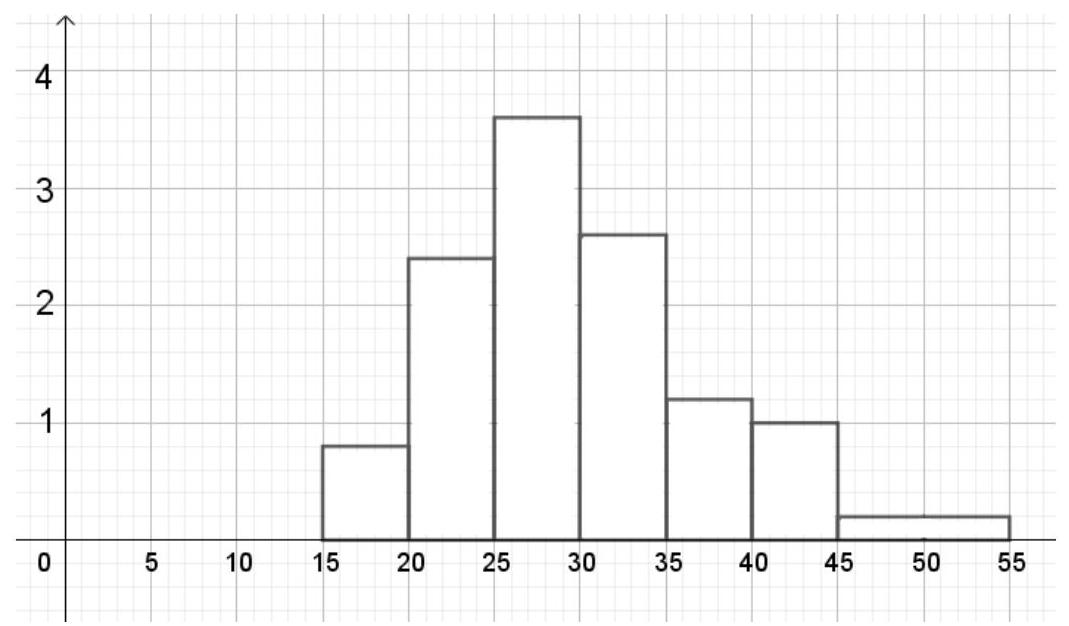
(a) Write down the labels that should appear on the two axes of the histogram.

 Hint

 Solutions

(b) Calculate estimates of the mean and standard deviation of the data, giving your answers correct to 2 decimal places. Hence identify any outliers, explaining your method.

 Hint

 Solutions

A similar survey of 60 diesel driven cars produced a mean of and a standard deviation of .
Use these statistics to compare the values of petrol and diesel cars five years after they were purchased as new.

 Hint

 Solutions

Questions 3 and 4 concern data from the 35 most populous countries in each of Asia and Europe for which data were available.

3. Fig 3.1 shows a scatter diagram of life expectancy at birth in , against life expectancy at birth in , for the 35 countries in Asia, along with the regression line. The correlation coefficient is 0.8457 .

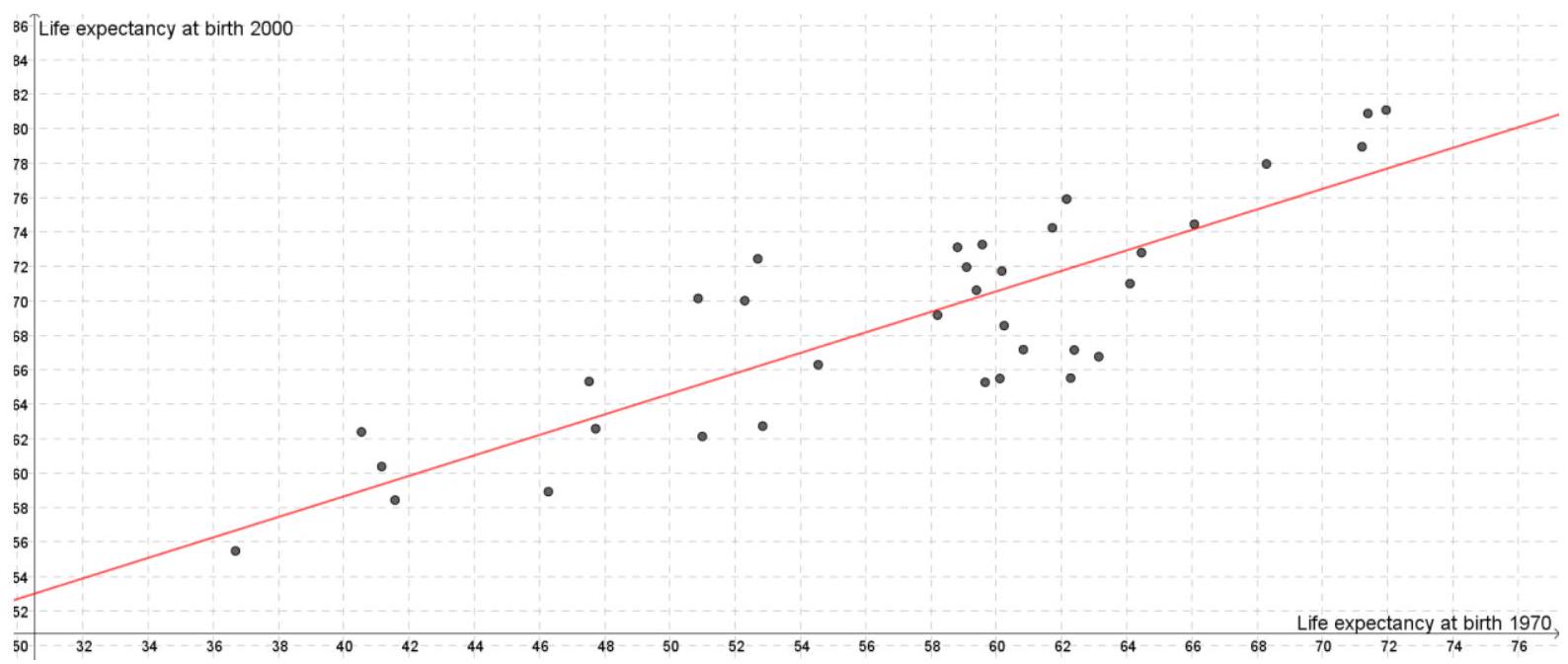
Figure 1: Fig 3.1

(a) Describe the association between life expectancy at birth in 2000 and life expectancy at birth in 1970 for these 35 countries in Asia.
(b) Given that the equation of the regression line is of the form , use Fig 3.1 to find the approximate value of .

Fig 3.2 shows a scatter diagram of life expectancy at birth in , against life expectancy at birth in , for the 35 countries in Europe. A regression line has also been drawn; it has equation .

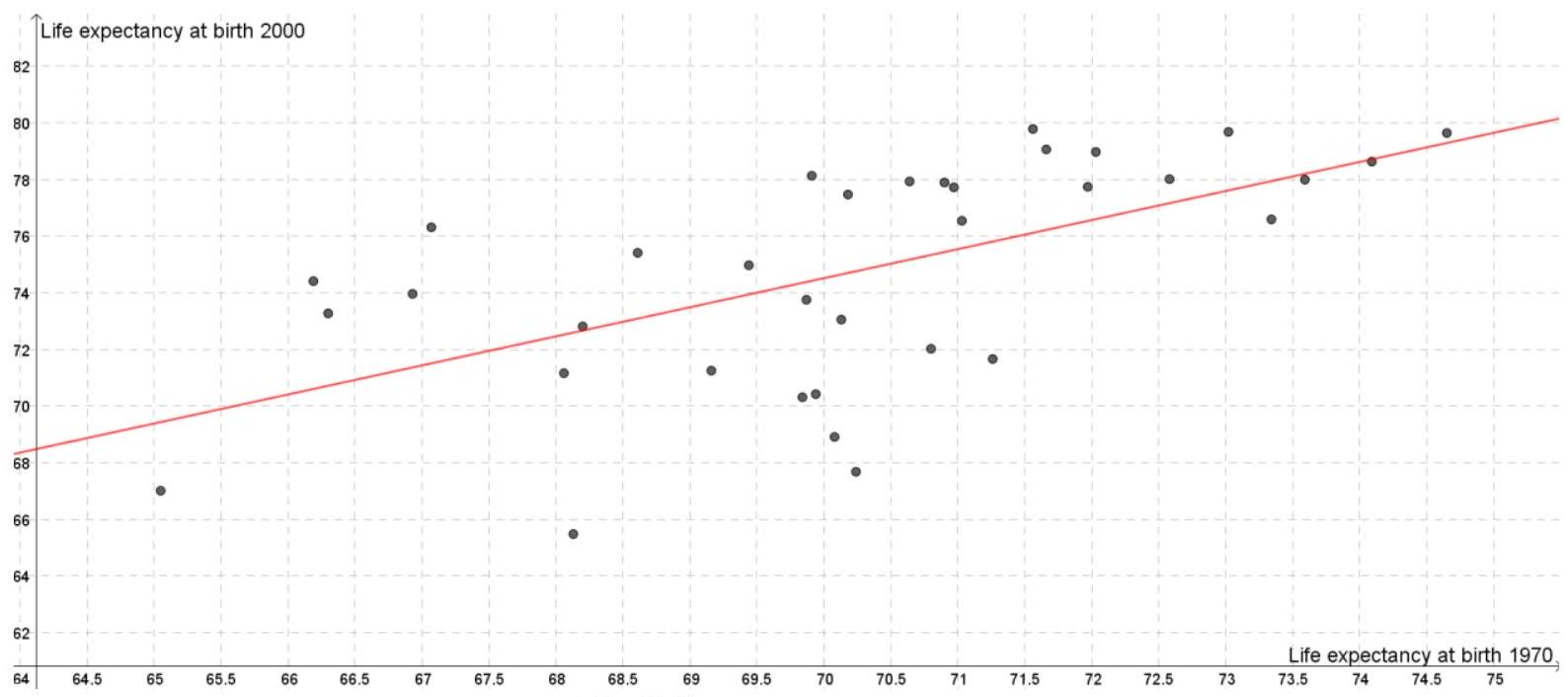
Figure 2: Fig 3.2

State, with a reason, whether the correlation coefficient is greater than or less than the correlation coefficient given for the Asian countries.
(d) Make one other comparison between the two sets of countries based on information in the scatter graphs.

4. The stem-and-leaf diagram below shows the most recent data for the median age, in years, of the population in each of the 35 countries in Europe. For example, there is one country in which the median age of the population is 47.4 years.

low:	33.4
37	0	1	2
38	2
39	3	8
40	3	5	8
41	0	1	1	5	5	6	9
42	5	5	5	6	7	7
43	0	0	1	3	7	9
44	0	2	2	9
45	8
46
47	4

Key: 3|1 means 3.1
(a) Find the values of the median, the lower quartile and the upper quartile for these data.
(b) Any value that is more than 1.5 multiplied by the interquartile range from the nearest quartile can be classed as an outlier. Use this definition of an outlier to show that the only outlier is 33.4 .

Table 4a shows summary statistics for the most recent data for the median age of the population in the 35 countries in Asia. The two countries in Asia with the highest median age are Japan ( 47.7 years) and Hong Kong ( 44.8 years). Two of the statistics are missing.

	35
Mean
	1048.3
	32942.71
Min	19
Q1	24.5
Median	29.9
Q3	33.1
Max	47.7

Table 1: Table 4a

Use the definition of an outlier as given in part (b) to show that Japan is the only outlier.

Fig. shows a box plot illustrating the median ages of the European countries

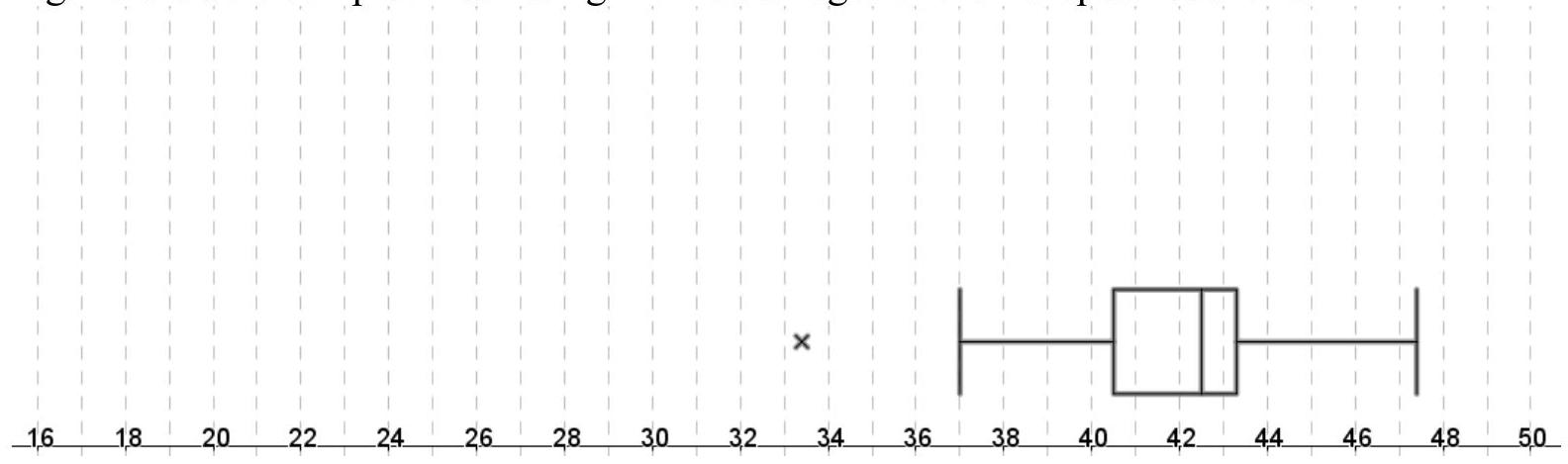
Figure 3: Fig. 4b

(d) On a copy of Fig. 4b, using the information given in Table 4a, draw a box plot for the median age in the Asian countries.
(e) Referring to the two box plots, make two comparisons between the data in the two regions.
(f) Calculate the values of the mean and the standard deviation for the Asian countries.
(g) An alternative definition of an outlier is a value that is more than 2 standard deviations from the mean. Show that this definition also makes Hong Kong an outlier.