Exponentials and Logarithms

1. Write as a single logarithm.
2. Express in terms of and .
3. Solve the following equations;
   (a)
   (b)
   
   giving your answers in exact form.
4. The temperature of the water in a kettle minutes after boiling is modelled by the equation .
   (a) What is the initial temperature of the water?
   (b) Find the temperature of the water after 5 minutes.
   Find the time at which the temperature of the water is .
   (d) Find the initial rate of cooling, and the rate of cooling after 2 minutes.
   (e) What will the long-term temperature of the water be?
5. In an experiment, the number of bacteria, , in a culture was estimated at time days after the experiment started.
   The results were as follows:

	1	2	3	4	5	6
	120	170	250	400	620	910

It is believed that the relationship between and can be expressed in the form

where and are constants.
(a) Use logarithms to draw a linear graph.
(b) Use your graph to estimate the values of and .
Estimate the number of bacteria present after 20 days. State, with a reason, whether your estimate is likely to be a good one.
6. The equation has one real root. What is the value of ?

7. It is believed that two quantities, and , are connected by a relationship of the form , where and are constants.
   In an experiment, the following data were produced.

	5	10	15	20	25	30	35
	9	24	48	69	102	131	166

To test the relationship Allegra has plotted the points on the graph below and drawn on a line of best fit:

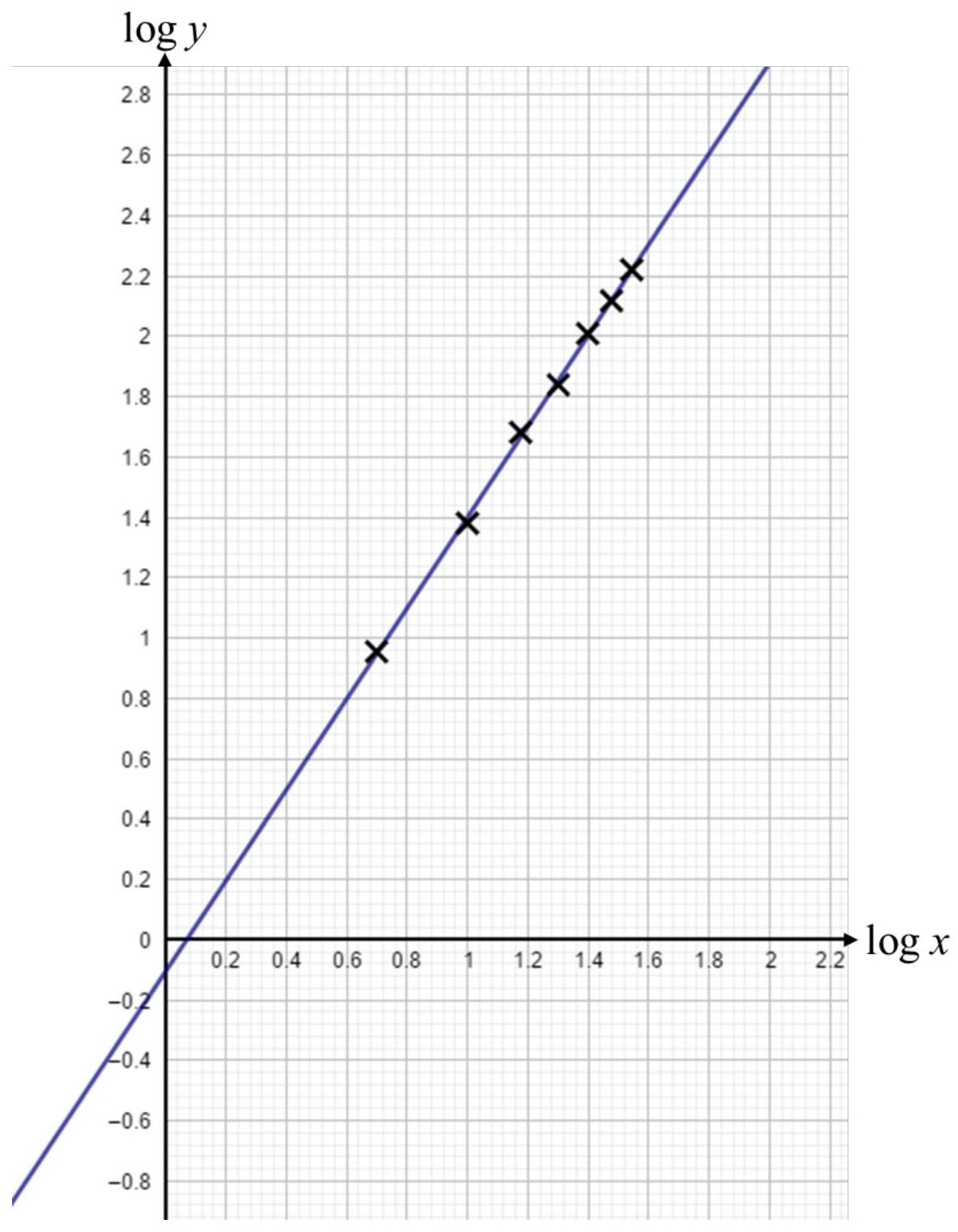
(a) Use Allegra’s graph to estimate the values of and .
(b) Use Allegra’s model to estimate the value of when .

Comment upon the reliability of this estimate.