Model for Friction

1. A box is at rest on a rough horizontal floor. A horizontal force of 400 N acts on the box and the box is on the point of moving. The coefficient of friction between the box and the floor is 0.65 . Calculate the weight of the box.

 Hint

Simply use the friction formula where is the applied force, is the coefficient of friction, and is the normal reaction force (which equals the weight of the box in this case).

 Solutions

To find the weight of the box, we first need to determine the normal reaction force between the box and the floor. The maximum frictional force that can act on the box before it starts to move is given by:

where is the coefficient of friction.
Given that the box is on the point of moving, the applied force of 400 N is equal to the maximum frictional force:

Solving for :

The normal reaction force is equal to the weight of the box, so:

Therefore, the weight of the box is approximately .

2. In the system below, the coefficient of friction between the block and the table is 0.2 .
   
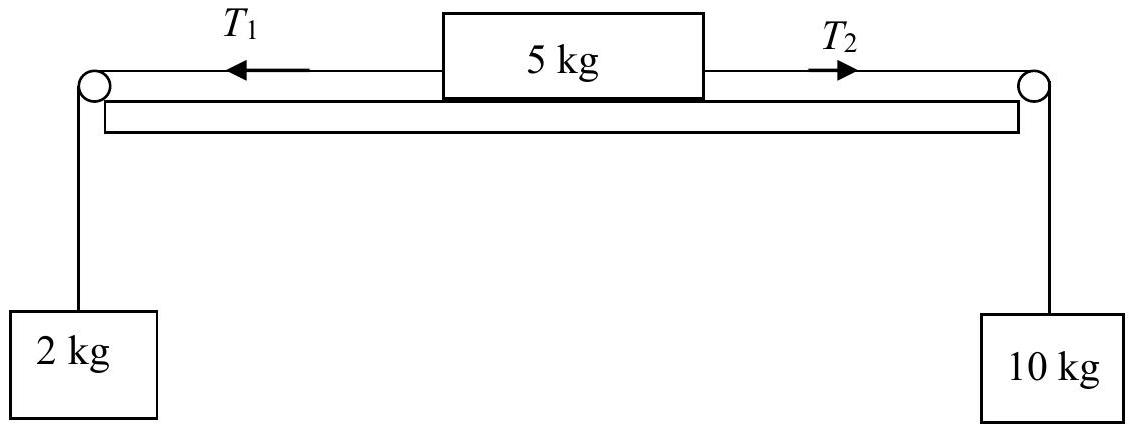
   Find the acceleration of the system and the tensions and .

 Hint

Firstly, we need to decide the direction of acceleration. Since 10kg is heavier than 2kg + 5kg, the system will accelerate such that the 10kg block moves downward, while the 2kg and 5kg blocks move to the right.

Then the key is to use Newton’s second law . We can consider three blocks separately or as a whole system. Analyses the forces acting on each block and set up equations accordingly
Net force on 2kg box = T1 - weight of 2kg box = 2a
Net force on 5kg box = T2 - T1 - frictional force = 5a
Net force on 10kg box = weight of 10kg box - T2 = 10a

We can solve these simultaneous equations to find the acceleration and tensions and .

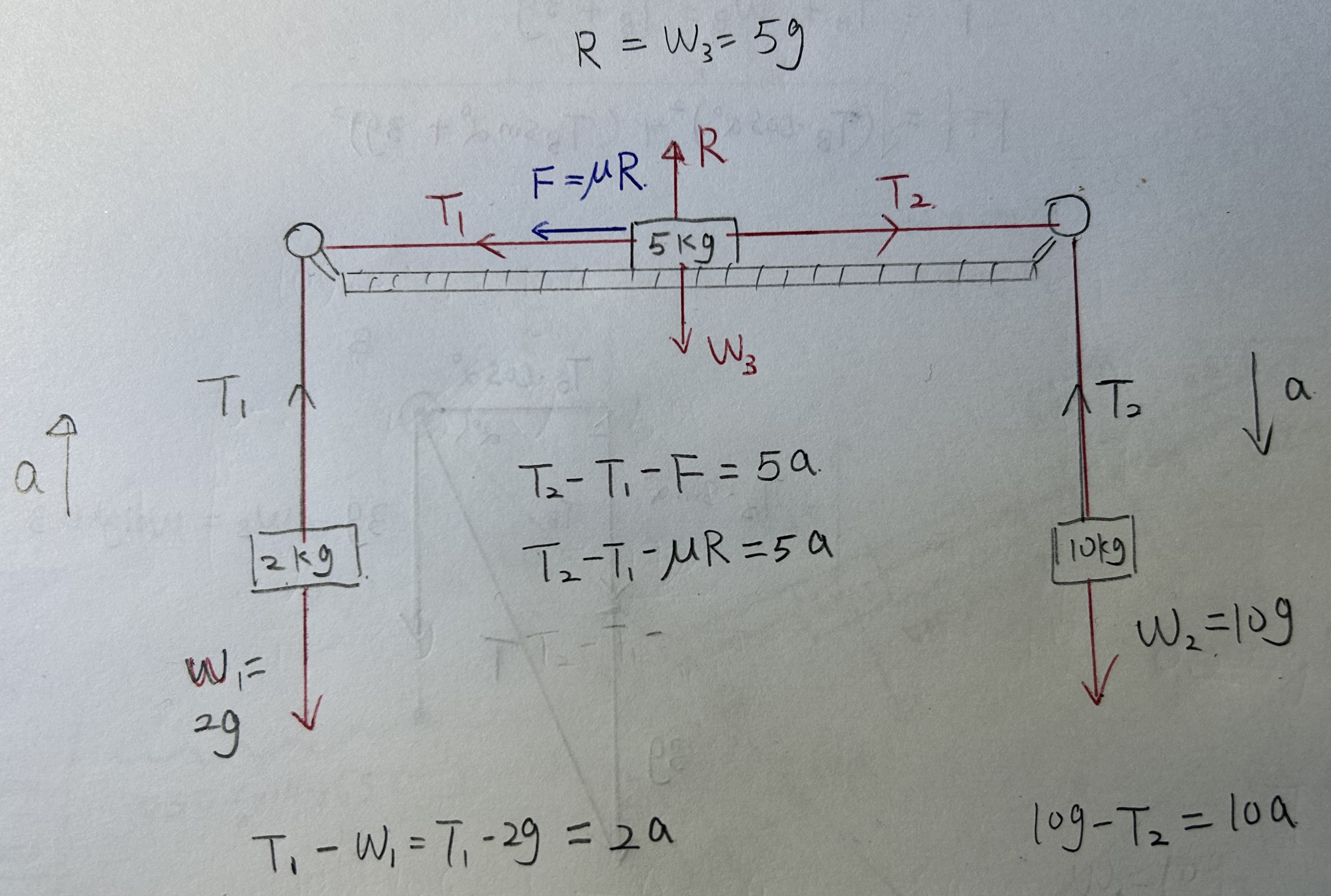
 Solutions

Firstly, we need to decide the direction of acceleration. Since 10kg is heavier than 2kg + 5kg, the system will accelerate such that the 10kg block moves downward, while the 2kg and 5kg blocks move to the right.

Then the key is to use Newton’s second law . We can consider three blocks separately or as a whole system. Analyses the forces acting on each block and set up equations accordingly
Net force on 2kg box = T1 - weight of 2kg box = 2a
Net force on 5kg box = T2 - T1 - frictional force = 5a
Net force on 10kg box = weight of 10kg box - T2 = 10a

Friction force on 5kg block = coefficient of friction × normal reaction = 0.2 × 5g = 0.2 × 5 × 9.8 = 9.8 N

We can solve these simultaneous equations to find the acceleration and tensions and .

If , we can solve these equations to find:

3. A small object of mass 4 kg is placed on a plane inclined at to the horizontal. It is held in place by a light inextensible string that is parallel to the plane, passes over a smooth pulley and is attached to a sphere of mass which hangs freely as shown in the diagram.
   
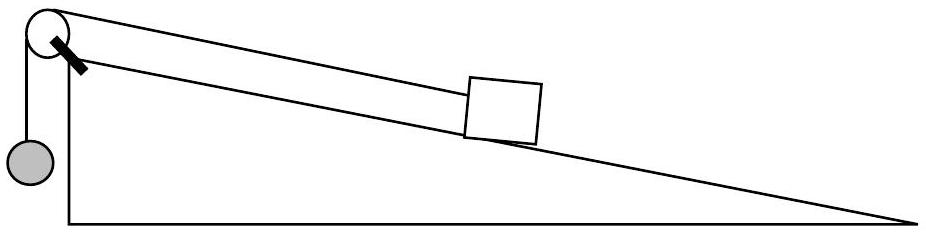
   (a) Rishi models the system with the modelling assumption that the plane is smooth. Calculate the value of for the system to be in equilibrium.

 Hint

 Solutions

To find the value of for the system to be in equilibrium, we need to analyze the forces acting on both the object on the inclined plane and the hanging sphere.
For the object on the inclined plane:

• The weight of the object is
• The component of the weight acting down the plane is
• The tension in the string acts up the plane.
  For the hanging sphere:
• The weight of the sphere is
• The tension in the string acts upward.
  For equilibrium, the forces must balance:

1. For the object on the inclined plane:
2. For the hanging sphere:

Setting the two expressions for equal gives:

Solving for :

Calculating :

Thus,

(b) Rishi finds that the system is in equilibrium when the mass of the sphere is 2.8 kg . He improves his model by modelling the plane as rough with coefficient of friction between the object and the plane. Find the range of values in which must lie. [5]

 Hint

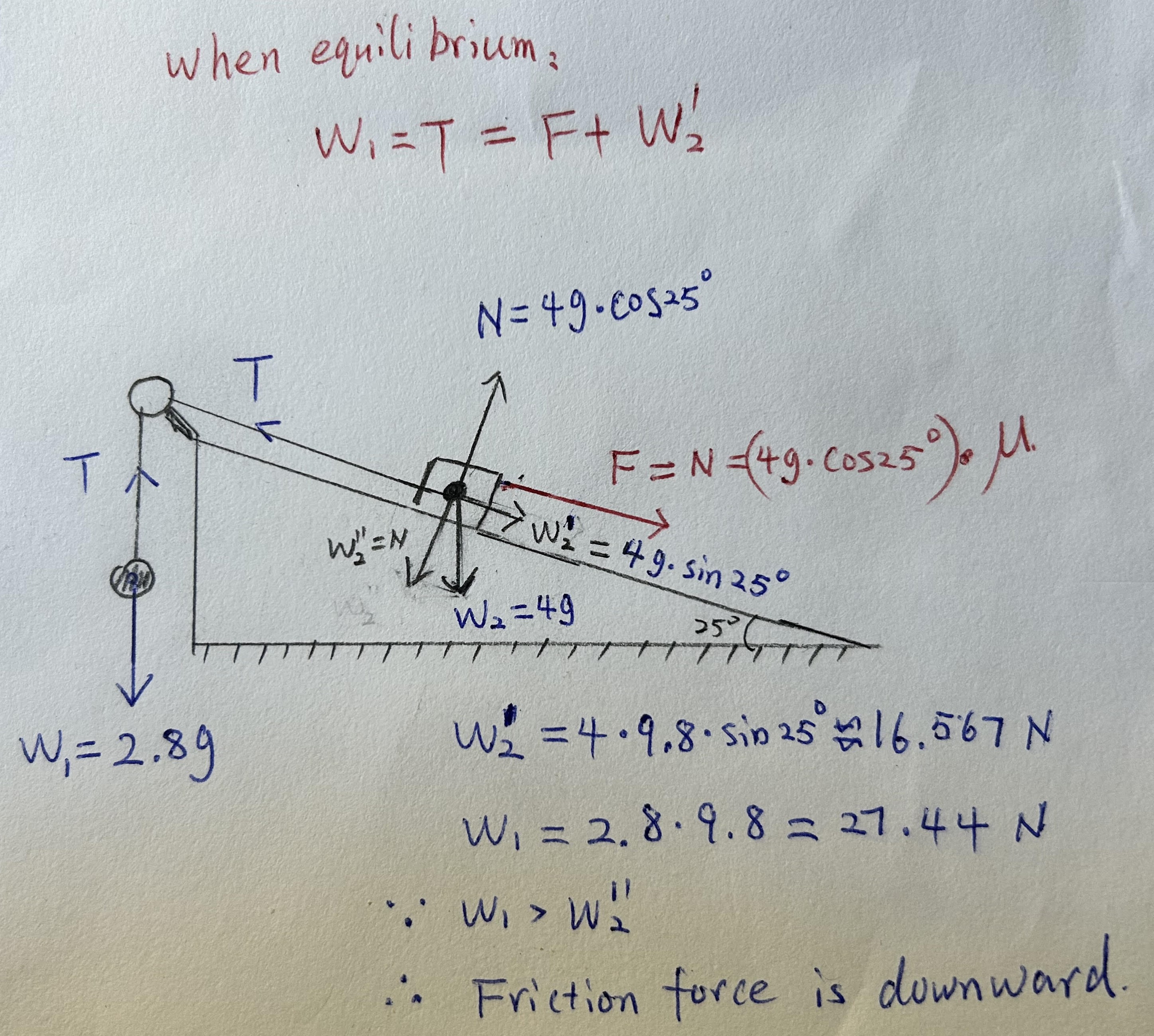
Need to decide the direction of frictional force first. Since the hanging mass is heavier than the previous case, the frictional force must act up the plane to prevent the object from sliding down.

Then set up the equations of equilibrium considering friction:

1. For the object on the inclined plane:
2. For the hanging sphere:

Then solve for using the frictional force formula , where is the normal reaction force.

 Solutions

To find the range of values for the coefficient of friction , we need to analyze the forces acting on the object on the inclined plane, considering friction.
For the object on the inclined plane:

• The weight of the object is
• The component of the weight acting down the plane is
• The normal reaction force is given by
• The frictional force acts up the plane and is given by
• The tension in the string acts up the plane.
  For the hanging sphere:
• The weight of the sphere is
• The tension in the string acts upward.
  For equilibrium, the forces must balance:

1. For the object on the inclined plane:
2. For the hanging sphere:

Setting the two expressions for equal gives:

Solving for :

Calculating this gives:

need to be at least this value to prevent the object from sliding up.
Therefore, the range of values for is:

4. The diagram shows a mass of 50 kg on a slope which makes an angle of with the horizontal. The coefficient of friction between the mass and the slope is 0.25 . You may assume that the mass does not tip up.
   
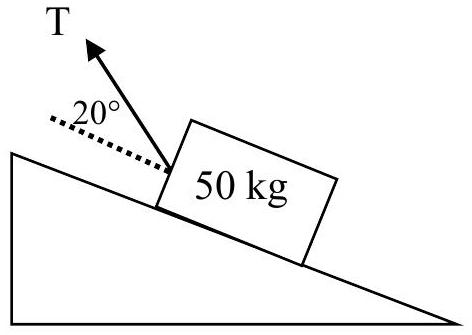
   Find the magnitude of the force if
   (a) the mass is about to move down the slope

 Hint

When the mass is about to move down the slope, the frictional force acts up the slope. Also the Reaction force need to consider the component of T perpendicular to the slope.

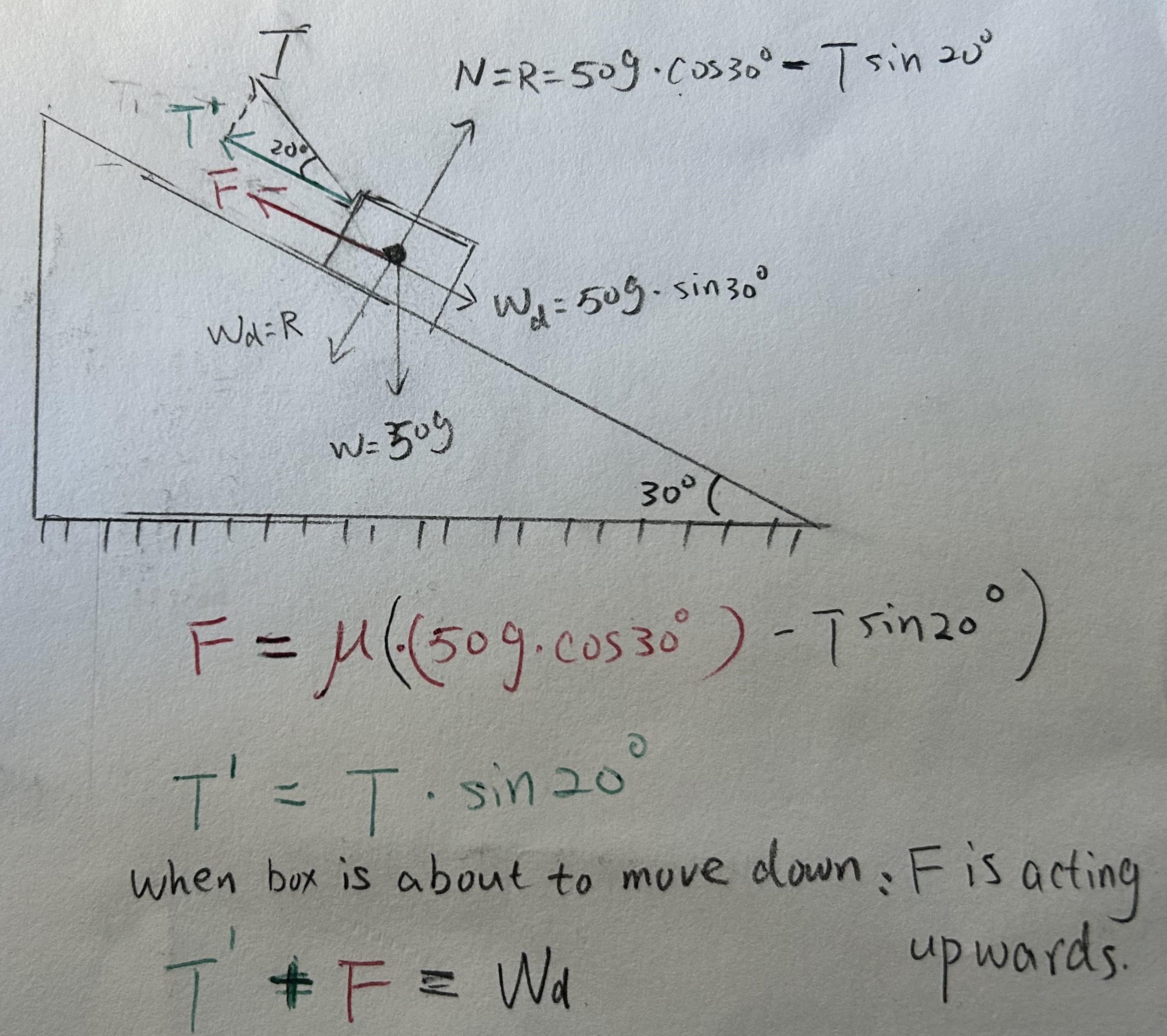
 Solutions

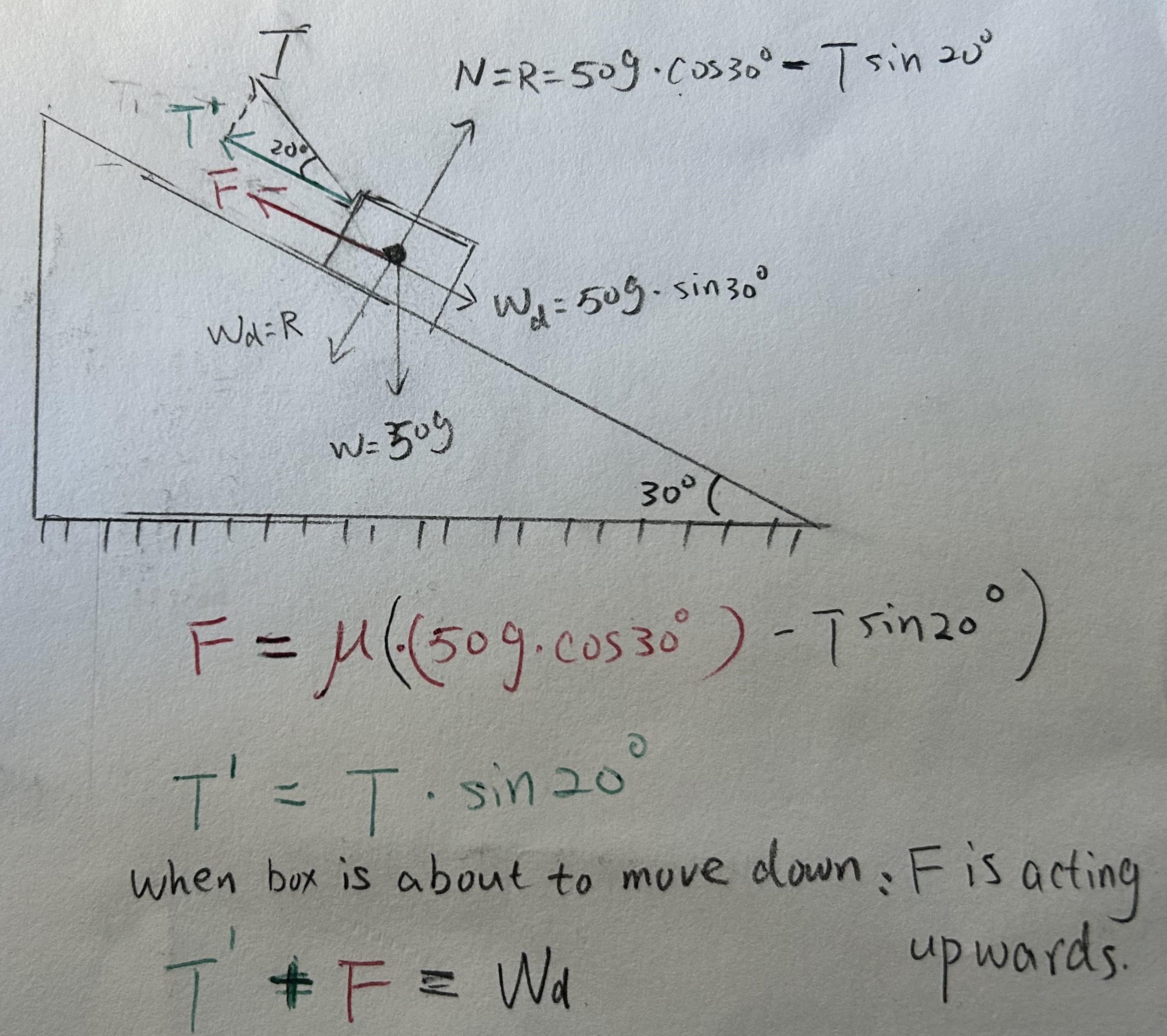
To find the magnitude of the force in both scenarios, we need to analyze the forces acting on the mass on the slope.
First, we calculate the weight of the mass:

Next, we resolve the weight into components parallel and perpendicular to the slope:

• The component of the weight acting down the slope is:
• The normal reaction force is:

The maximum frictional force that can act on the mass is given by:

the component of T alone the slope is:

When the mass is about to move down the slope, the frictional force acts up the slope, and the equation of motion along the slope is:

Substituting the values we have:

Solving for :

Calculating the right side:

Now, solving for :

Calculating the left side coefficient:

Thus,

(b) the mass is accelerating at up the slope.

 Hint

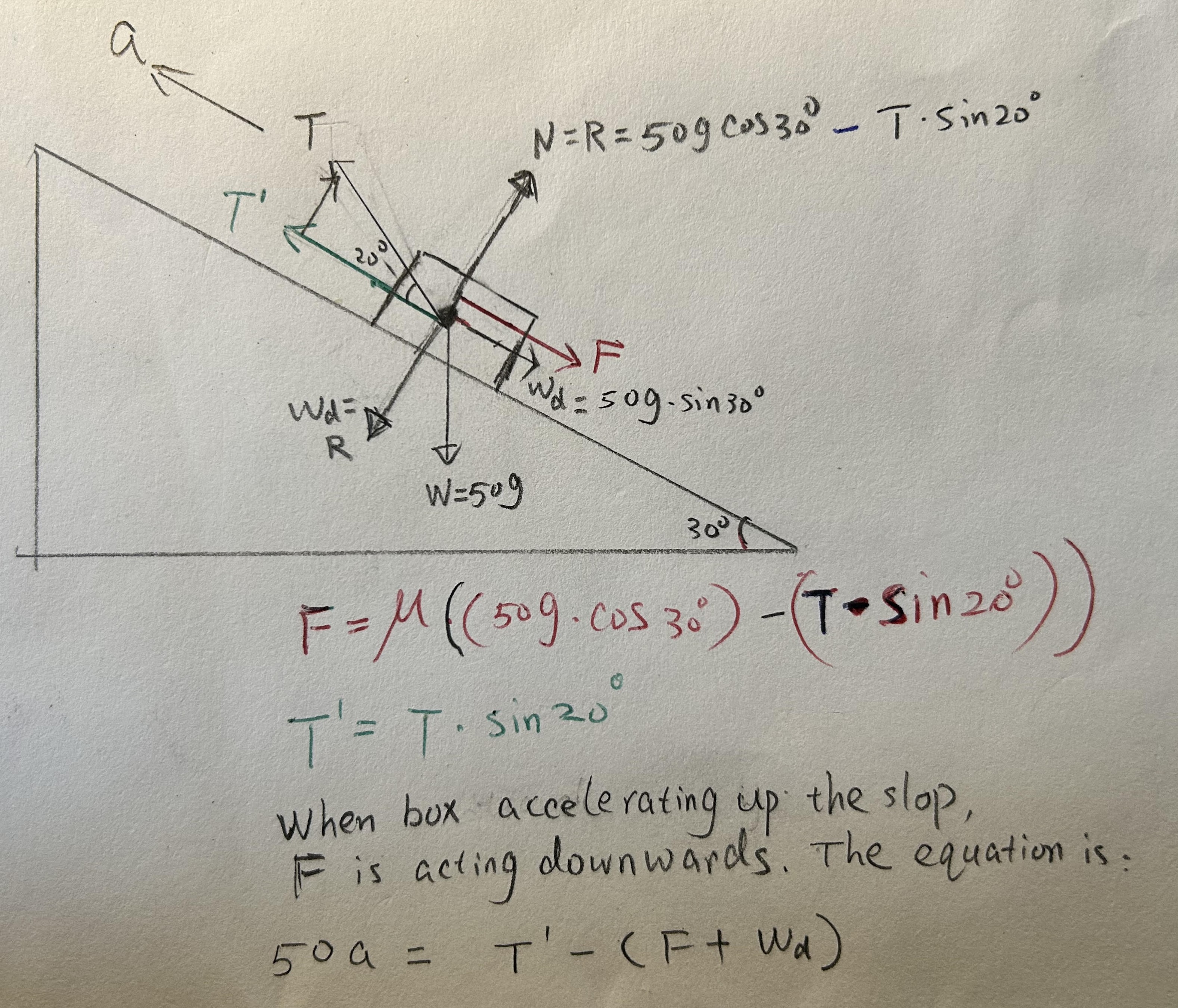
Same as part (a), but now consider the acceleration up the slope. The frictional force will act down the slope in this case.
The Reaction force need to consider the component of T perpendicular to the slope.

 Solutions

To find the magnitude of the force when the mass is accelerating up the slope at , we need to consider the forces acting on the mass along the slope.
The box is moving up the slope, so the frictional force acts down the slope.
the component of T alone the slope is:

The net force acting on the mass along the slope is given by Newton’s second law:

The equation of motion along the slope is:

Substituting the known values:

Solving for :

Now, solving for :

Calculating the right side:

Calculating the left side coefficient:

Thus,

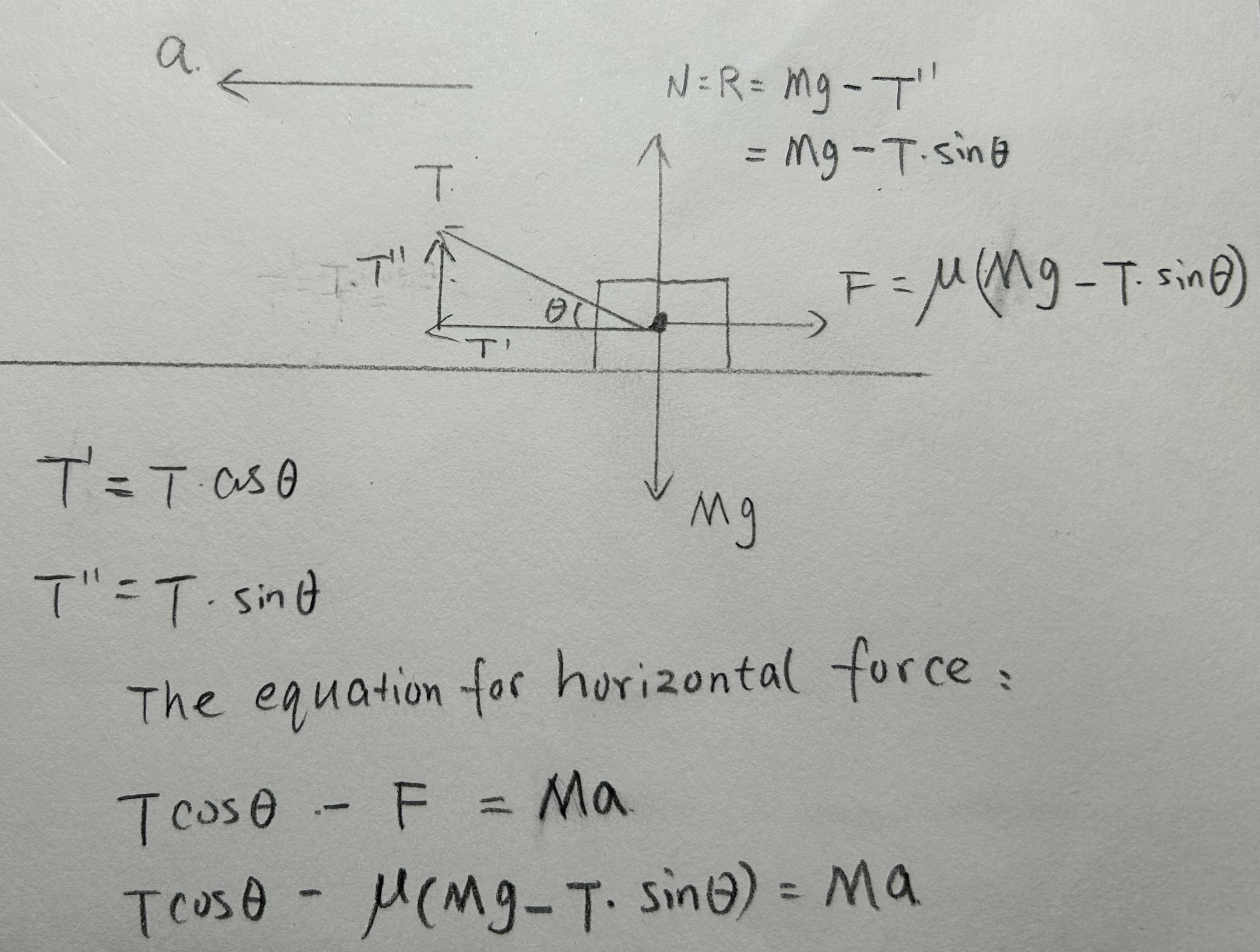
5. George pulls a crate of mass across a rough horizontal floor using a light inextensigle string which makes an angle to the horizontal. The coefficient of fricton between the floor and the box is . The acceleration of the box across the floor is . George models the situation assuming that there are no other resistive forces.
   (a) Show that , the tension in the string is given by .

 Hint

Similar to previous questions, when calculating the friction force, we need to include the vertical component of the tension when calculating the normal reaction force.

 Solutions

To derive the expression for the tension in the string, we need to analyze the forces acting on the crate both horizontally and vertically.

1. Vertical Forces:

• The weight of the crate acts downward:
• The vertical component of the tension in the string acts upward:
• The normal reaction force from the floor acts upward.
  The equation for vertical forces is:

Solving for :

2. Horizontal Forces:

• The horizontal component of the tension in the string acts to the right:
• The frictional force acts to the left and is given by
  The equation for horizontal forces is:

Substituting with :

Expanding and rearranging gives:

Combining the terms with :

Solving for :

Factoring out :

(b) George knows that when and , the box is on the point of moving. Use the expression from part (a) to calculate a value of .

 Hint

When box is about to move, the frictional force is at its maximum value and the acceleration is zero.

 Solutions

When box is about to move, the frictional force is at its maximum value and the acceleration is zero. Therefore, we can set in the expression for derived in part (a):

Substituting the known values , , , and :

Rearranging to solve for :

Expanding the left side:

Rearranging gives:

Solving for :

Calculating the values:

6. Two small blocks of mass 0.8 kg and 1.2 kg are attached with a light inextensible rod which is parallel to the bases of the blocks. The blocks are placed on a plane inclined at to the horizontal with the 1.2 kg block higher than the 0.8 kg block. The coefficient of friction between the 0.8 kg mass and the plane is 0.5 and that between the 1.2 kg mass and the plane is 0.3 .
   
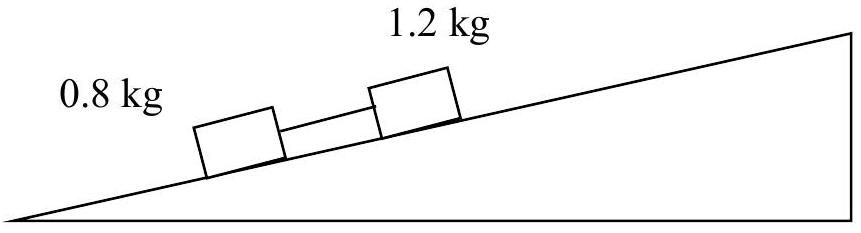
   (a) Determine the acceleration of the system.

 Hint

Try to work out the frictional forces and downward forces acting on both blocks. The net force on the system will be the difference between the total downward forces and the total frictional forces. Then use Newton’s second law to find the acceleration of the system.
Heavier box is higher, so the system will accelerate down the slope.

 Solutions

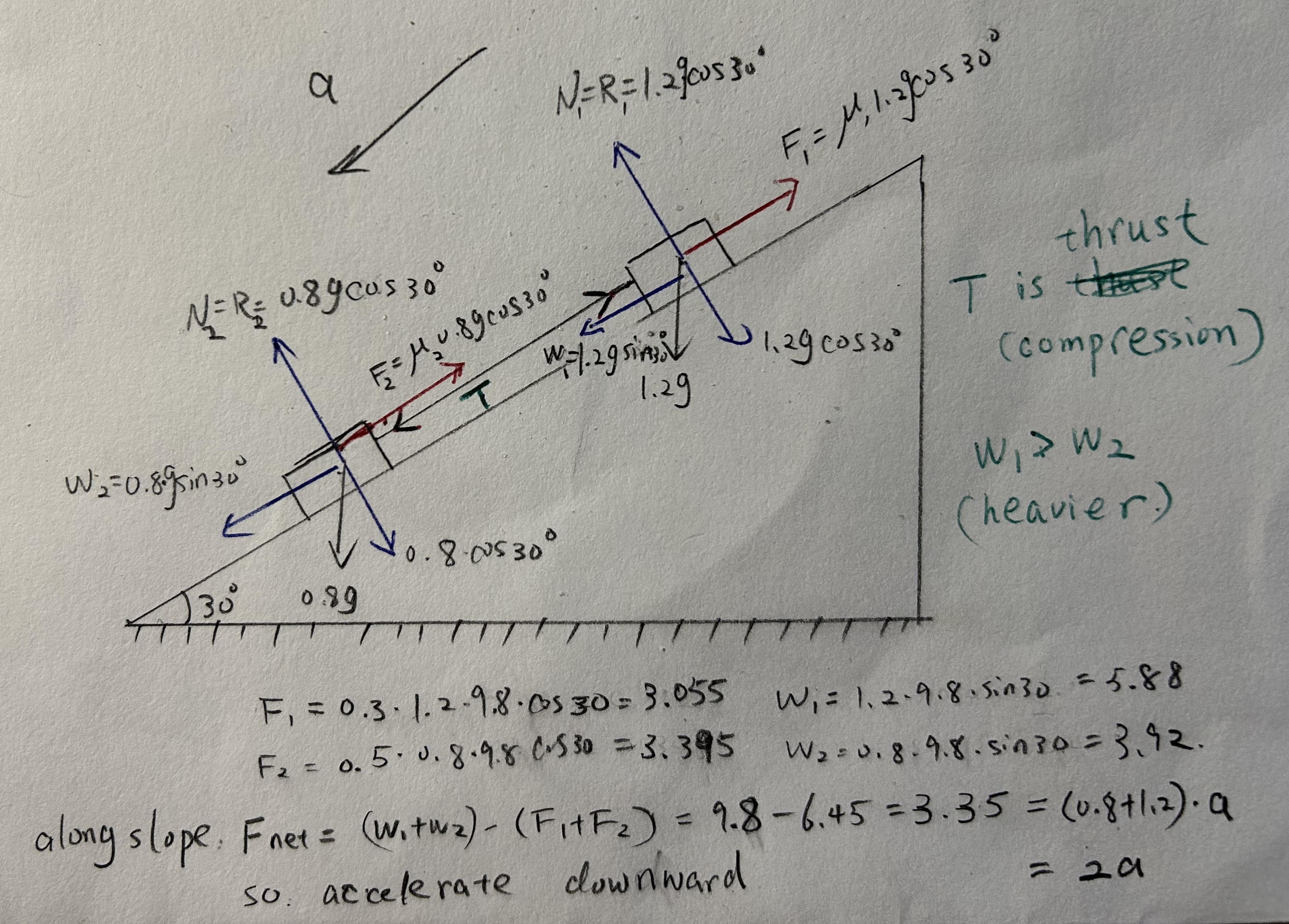
To determine the acceleration of the system, we first need to calculate the forces acting on both blocks.

1. For the 0.8 kg block:

• Weight:
• Component of weight down the slope:
• Normal reaction force:
• Frictional force:

2. For the 1.2 kg block:

• Weight:
• Component of weight down the slope:
• Normal reaction force:
• Frictional force:

3. Net Force on the System:

• Total downward force:
• Total frictional force:
• Net force:

4. Acceleration of the System:

• Total mass of the system:
• Using Newton’s second law:

(b) Determine the magnitude of the force in the rod making clear whether it is in tension or compression.

 Hint

Since 1.2g box is heavier, the rod will be in thrust (compression). Consider the forces acting on either block and use Newton’s second law to find the force in the rod.

 Solutions

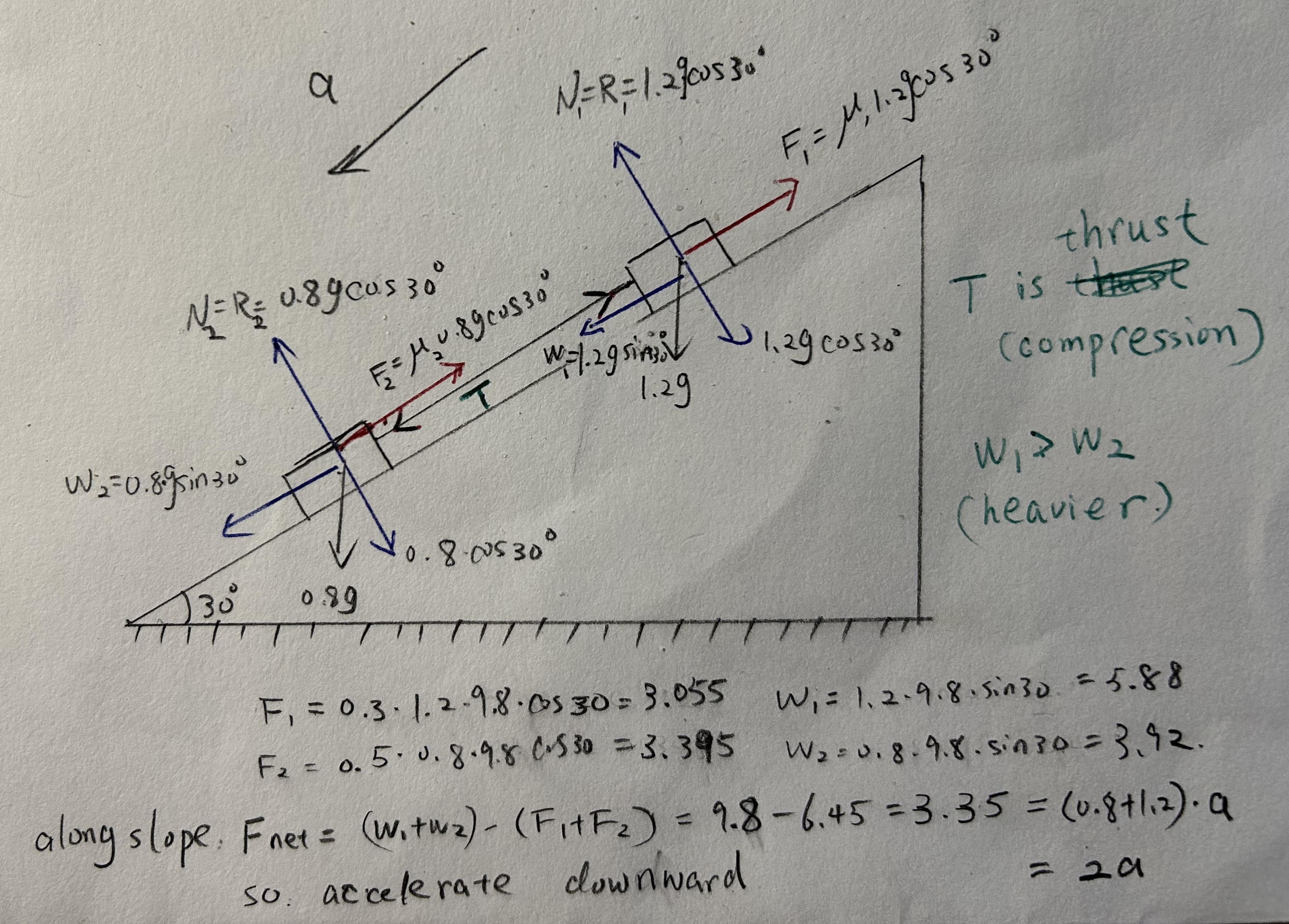
To determine the magnitude of the force in the rod, we can analyze the forces acting on either block. Let’s consider the 0.8 kg block.

1. For the 0.8 kg block:

• Weight component down the slope:

• Frictional force:

• Acceleration of the block:

Using Newton’s second law for the 0.8 kg block:

The force on Rod is compression (thrust), so we have:

Substituting the known values:

Solving for :