Variable Acceleration

- A racing car accelerates from rest along the track. Its speed,
, is modelled for the first four seconds of its motion by
(a) Find an expression for the distance travelled by the car in the first
Hint
Solutions
The speed is given by
The distance travelled in the first
Thus
with
(b) Calculate the distance travelled from
Hint
Solutions
Recall
Hence
and
The distance travelled from
Hint
Solutions
Differentiate v with respect to t:
Factor out 3 and factor the quadratic:
Hence k=3.
- A particle moves on the
-axis. Its displacement, , from the origin O is given by , where is the time in seconds.
How far is the particle from O when it is instantaneously at rest?
Hint
Get the velocity by differentiating the displacement first. Then set the velocity to zero to find the time when the particle is at rest. Finally, substitute this time back into the displacement equation to find how far the particle is from O.
Solutions
Differentiate
Set
Substitute
The particle is
- At
a particle travels through point P with a velocity of . The acceleration of the particle is given by .
(a) Find the times when the velocity,, is .
Hint
For variable acceleration, integrate the acceleration function to find the velocity function. Use the initial velocity condition to find the constant of integration. Then set the velocity function equal to -18 and solve for t.
Solutions
Integrate the acceleration function to find the velocity function:
Use the initial condition
Thus, the velocity function is:
Set
Rearranging gives:
Multiply through by 10 to eliminate decimals:
Using the quadratic formula:
Thus, the two solutions for
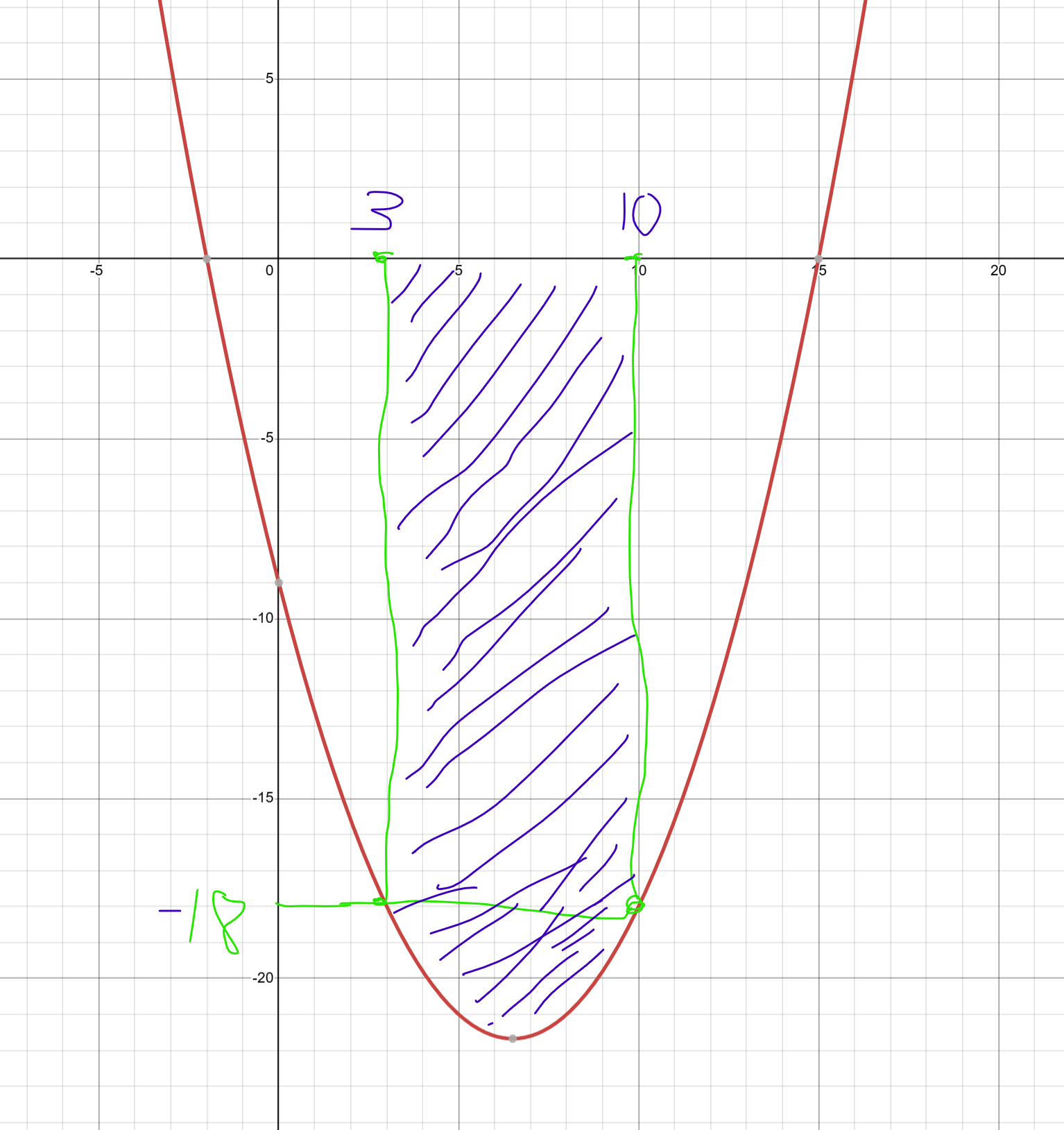
(b) Find the distance covered by the particle when
Hint
To find the distance covered when
Basically, the distance covered is the area under the velocity-time graph between the times when
Basically, the distance covered is the area under the velocity-time graph between the times when
Solutions

From part (a), we found that
To find the distance covered when
The velocity function is:
To find the distance covered when
The velocity function is:
Integrate the velocity function to find the displacement:
We can ignore the constant of integration
Now, calculate the displacement from
Calculating each term:
For
For
For
Now, find the distance covered, the area is under the x axis so it will be negative, we make it positive for distance:
The distance covered by the particle when
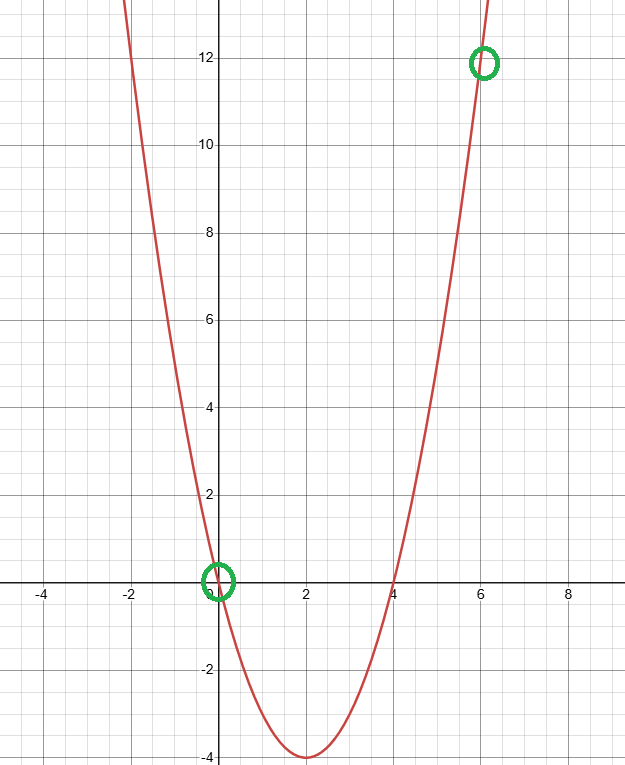
- An insect moves in a straight line. The time,
, is in seconds and distance travelled is in metres.
The velocity,
You are also given that
(a) Show that
(a) Show that
Hint
C is the constant velocity between
Solutions
to find
Thus,
(b) Calculate the values of
Hint
Need to setup two equations using the information given. One equation comes from the fact that the velocity at
Solutions
From part (a), we have
At
At
At
Subtract equation (1) from equation (2):
Substituting
Thus,
The motion of the insect in the interval
The motion of the insect in the interval
This indicates that the insect is decelerating linearly over this time period. The decelerating is constant.
Hint
quadratic curve in the interval
Solutions
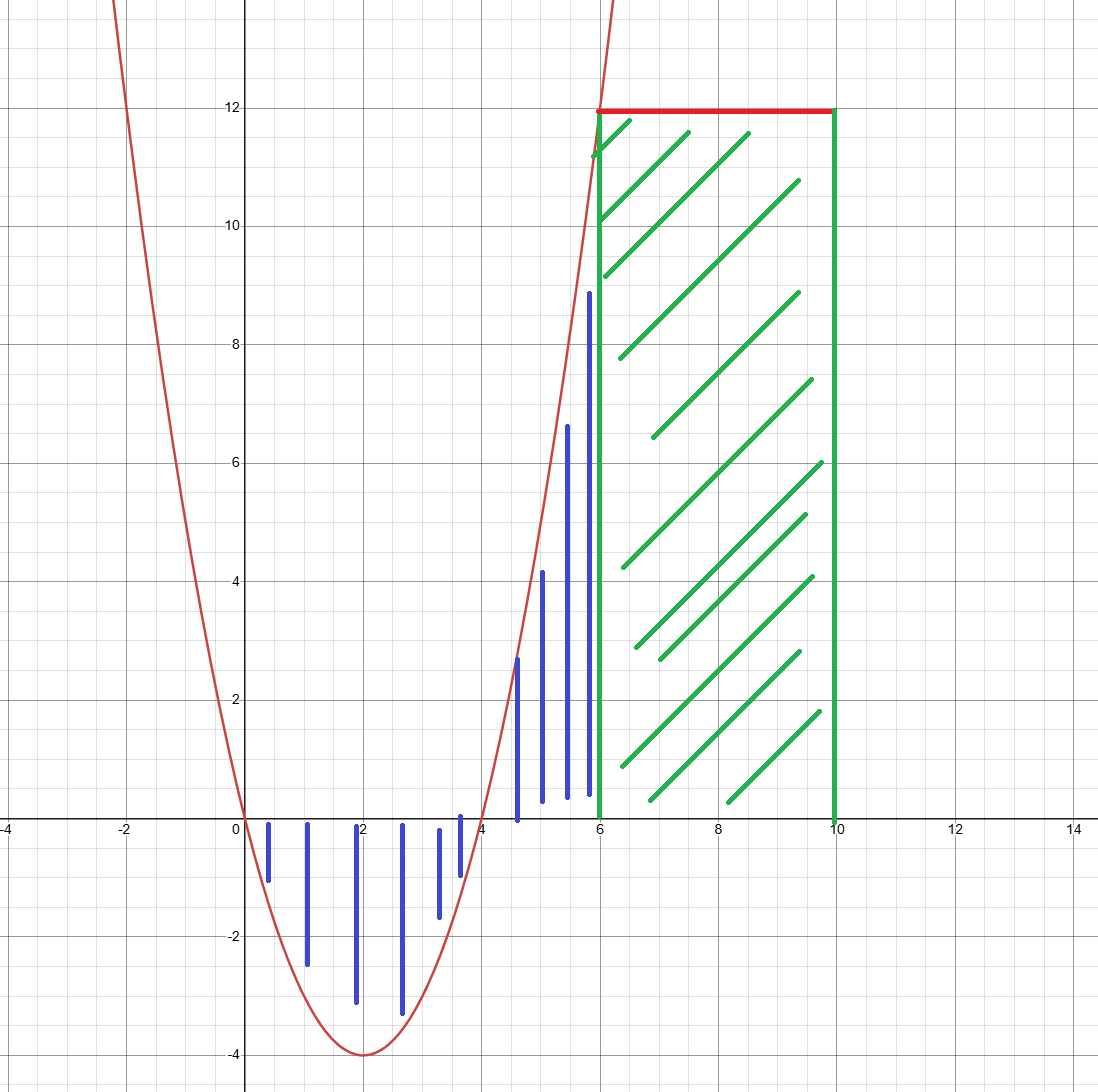
(d) Calculate the distance travelled by the insect in the interval
Hint
The distance travelled is the area under the velocity-time graph from
There are two parts to this area: from
First part can be found by integrating the velocity function from
There are two parts to this area: from
First part can be found by integrating the velocity function from
Solutions

Since between
First, calculate the distance from
integrate the velocity function:
First, calculate the distance from
integrate the velocity function:
The distance is the absolute value:
Next, calculate the distance from
Now, calculate the distance from
The velocity is constant at
The velocity is constant at
The total distance travelled from
- The motion of a particle is represented on the velocity time graph shown below. The motion is given by the equations:
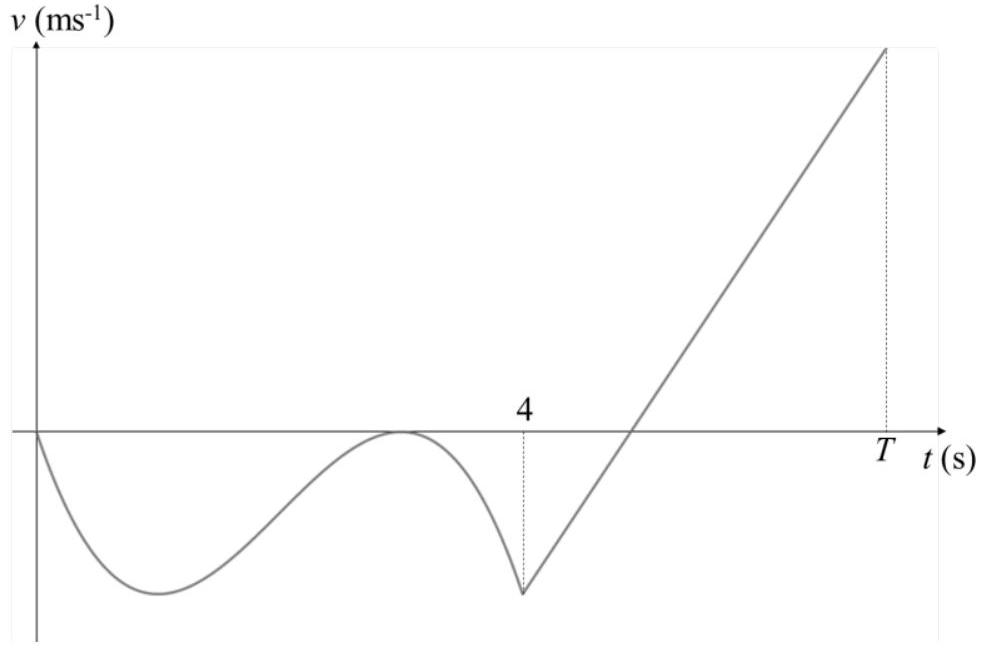
The particle returns to its starting position at time
Find the velocity of the particle at time
Find the velocity of the particle at time
Hint
The particle returns to its starting position when the total displacement is zero. So we need to find the expressions for displacement by integrating the velocity function. Then, set the total displacement to zero and solve for
Then substitute
There are two parts to the displacement: from
Solutions
First compute the displacement from 0 to 4:
Displacement is negative, showing in the graph that the area are under x axis.
Continuity of velocity at t=4 gives
so
and for
Let
Evaluating the integral gives
hence
The relevant root (with
Finally the velocity at T is
Numerically v(T)≈7.86 ms⁻¹.
