Kinematics

Use unless stated otherwise.

1. A particle traveling in a straight line at is brought to rest by a constant deceleration in a distance of 22.5 m . Find the time taken for the particle to come to rest.

 Hint

Just use the SUVAT equation that does not involve time to find the acceleration first, then use that to find the time.

 Solutions

Using the SUVAT equation we have

Using we have

2. A plant pot falls from a balcony. It hits the ground after 2.24 seconds.
   (a) By modelling the plant pot as a particle, find the height of the balcony from the ground.

 Hint

Use the SUVAT equation that does not involve final velocity to find the height.

 Solutions

Using the SUVAT equation we have

(b) State one further assumption used to model this situation.

 Solutions

Assume that air resistance is negligible.

3. A particle accelerates uniformly from to in 8 s . How far does it travel in this time?

 Hint

Use the SUVAT equation that involves initial velocity, time and acceleration to find the distance. Find the acceleration first using the equation that involves initial velocity, final velocity and time.

 Solutions

Using the SUVAT equation we have

Using we have

4. A particle is projected at a speed of up a straight inclined track. Whilst on the track the particle experiences a constant acceleration down the track of . Find the length of time that the displacement of the particle up the track from the point of projection is greater than 8 metres.

 Hint

Again use the SUVAT equations. Find the time taken to reach 8 metres by rearranging the equation to form a quadratic equation.
There will be two solutions, find the difference between them to get the time spent above 8 metres.

 Solutions

Using the SUVAT equation we have

Solving this quadratic equation gives or
The displacement of the particle up the track from the point of projection is greater than 8 metres for

5. A train passes through station A tramelling at along a straight track.

For the first 5 seconds after leaving the station the train has a constant acceleration of .

The train then travels with constant velocity for a time, T , until it decelerates uniformly for 15 seconds, coming to rest at the station which is 2.68 km away from .

Sketch a velocity time graph for the motion of the train and calculate the time taken to get between the two stations.

 Hint

There are three phases to the motion: acceleration, constant velocity and deceleration.

 Solutions

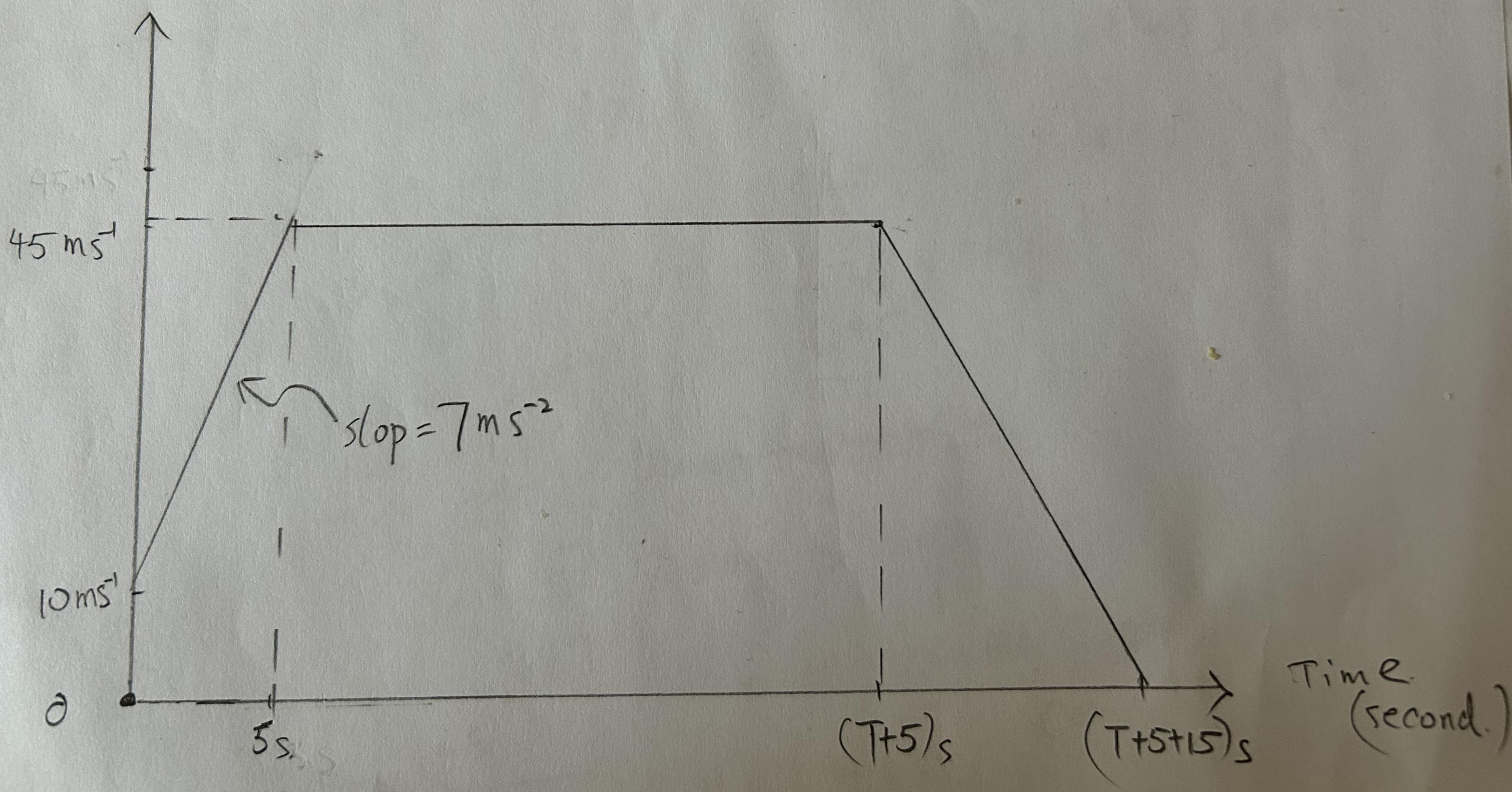
Phase 1 (0 → 5 s): initial speed

Phase 2 (constant velocity): speed for time ,

Phase 3 (braking for 15 s to rest):
initial speed

Total displacement:

so

Hence

Total time:

Answer: 69 s.

6. A particle travels in a straight line.
   The motion is modelled by the - diagram below.
   
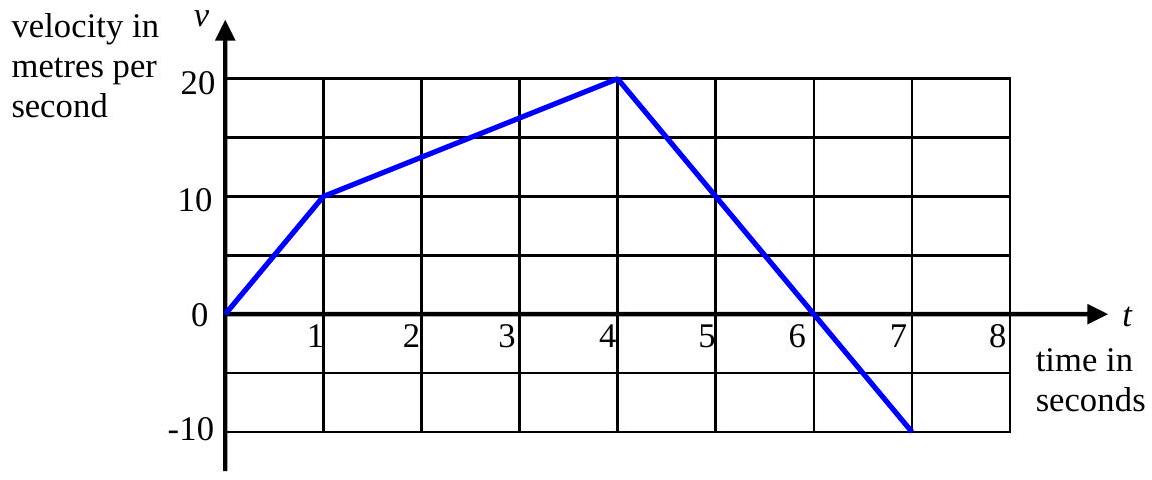
   (a) Calculate the acceleration of the particle in the part of the motion from to .

 Hint

The acceleration over that interval is the slope of the v–t graph.

 Solutions

The acceleration is given by the gradient of the - graph.
From to , the change in velocity is and the change in time is .
Therefore, the acceleration is .

(b) Calculate the displacement of the particle from its position when to its position when .

 Hint

There are three sections above the time axis and one section below it. To calculate displacement, calculate the area of each section and add them up, then subtract the area below the time axis.

 Solutions

7. A ball A is thrown vertically upwards at from a point P . Three seconds later a second ball is also thrown vertically upwards from the point at . Taking the acceleration due to gravity to be , calculate
   (a) the time for which ball A has been in motion when the balls meet

 Hint

Let the time after ball A is thrown when they meet be seconds. need to be greater than 3 seconds since ball B is thrown 3 seconds later.

The displacements of ball A and ball B are same.

 Solutions

Setting :

Hence ball A has been in motion for s when the balls meet.

(b) the height above P at which A and B meet.

 Hint

Use either displacement equation for ball A or ball B to find the height when they meet.

 Solutions

Considering ball A, the displacement when they meet is:

8. Cars A and B are traveling in the same direction along a straight road. The time is in seconds.
   At , car A is at rest. It accelerates at for and then travels at a constant speed.
   Car B travels at for and then accelerates at until it reaches a speed of , after which it continues at this constant speed.
   (a) Draw - diagrams for the motion of car A and of car B , where is the speed in and .

 Solutions

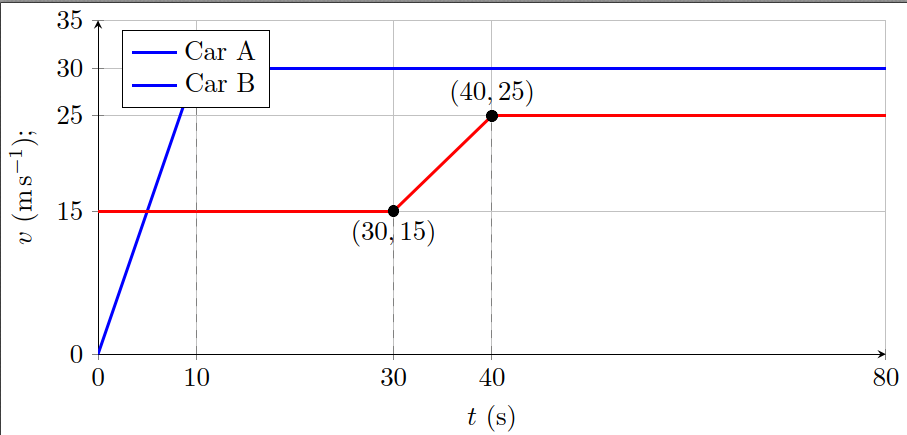
(b) Show that, in the first 40 seconds, car A travels 400 m further than car B.

 Hint

Calculate the displacements of each car in the first 40 seconds using the area under the v–t graphs.

 Solutions

For car A (accelerates at ) for ; then constant speed for ):

For car B (constant for ; then accelerates from to over ):

Therefore the difference in the first 40 s is

so car A travels further than car B in the first 40 seconds.

Given that car A is 500 m behind car B at , at what value of does car A catch up with car B ?

 Hint

From part (b), car A catches up 400 meters at s. In other words, the gap has closed from 500 m to 100 m after 40 s.
After that, both cars travel at constant speeds. Find the time taken for car A to close the remaining 100 m gap.

 Solutions

Given that car A is initially behind car B, A catches B when the gap closes to zero.

From the previous kinematic results at :

so the separation closed in the first 40 s is

Thus the remaining separation at is

For both cars move at constant speeds and , so the relative speed is

Time to close the remaining is

Hence A catches B at

Therefore car A catches car B at .