Probability

- In this question you must show detailed reasoning.
Which is more likely, never getting a 6 when rolling a fair die six times, or never getting a double 6 when rolling a pair of fair dice 36 times?
2. In the sixth form at Eastport School, there are 45 students studying at least one of the three sciences, Biology, Chemistry and Physics.
2. In the sixth form at Eastport School, there are 45 students studying at least one of the three sciences, Biology, Chemistry and Physics.
The diagram below shows the number of students studying each science.
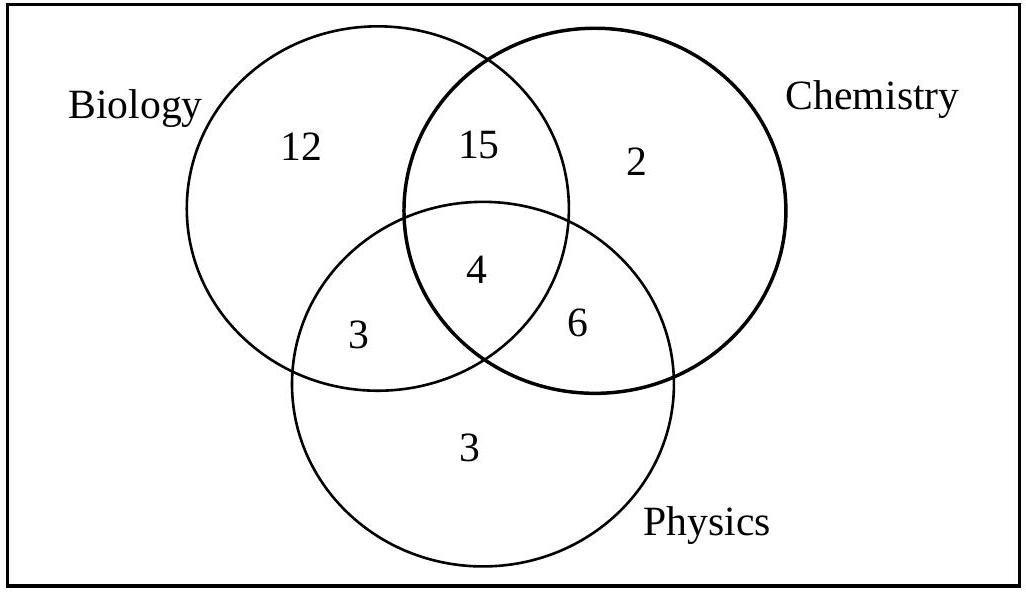
(a) Find the probability that one of these students, selected at random, is studying
(i) Physics
(ii) Chemistry
(iii) both Physics and Chemistry.
(b) Two students are selected at random. Find the probability that both are studying just one science and that they are not both studying the same science.
3. The probability distribution of a discrete random variable

(a) Find the probability that one of these students, selected at random, is studying
(i) Physics
(ii) Chemistry
(iii) both Physics and Chemistry.
(b) Two students are selected at random. Find the probability that both are studying just one science and that they are not both studying the same science.
3. The probability distribution of a discrete random variable
(a) Show that
Two values of
(b) Find the probability that the product of the two values is even.
(b) Find the probability that the product of the two values is even.
- The Venn diagram shows two events, A and B , and their associated probabilities.
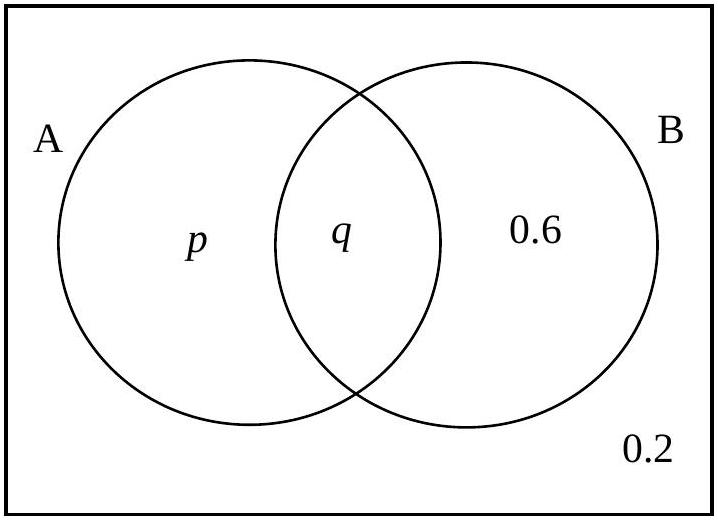
Given that events A and B are independent, find the values of
5. The students in a school sixth form were asked for their most common mode of transport to school. The replies are summarised in the table below.
5. The students in a school sixth form were asked for their most common mode of transport to school. The replies are summarised in the table below.
| Mode of transport | Total | ||||||
| Walk/Cycle |
|
Private car | |||||
| Year Group | Year 12 | 44 | 72 | 16 | 132 | ||
| Year 13 | 40 | 63 | 17 | 120 | |||
| Total | 84 | 135 | 33 | 252 | |||
(a) Two students are randomly selected. What is the probability that they are in different year groups?
(b) Two students are randomly selected. What is the probability that they are in different year groups but are in the same ‘mode of transport’ category?
6. A practical music examination can be taken once or twice. Those candidates who fail it on the first occasion take it a second time.
(b) Two students are randomly selected. What is the probability that they are in different year groups but are in the same ‘mode of transport’ category?
6. A practical music examination can be taken once or twice. Those candidates who fail it on the first occasion take it a second time.
For those having their first attempt,
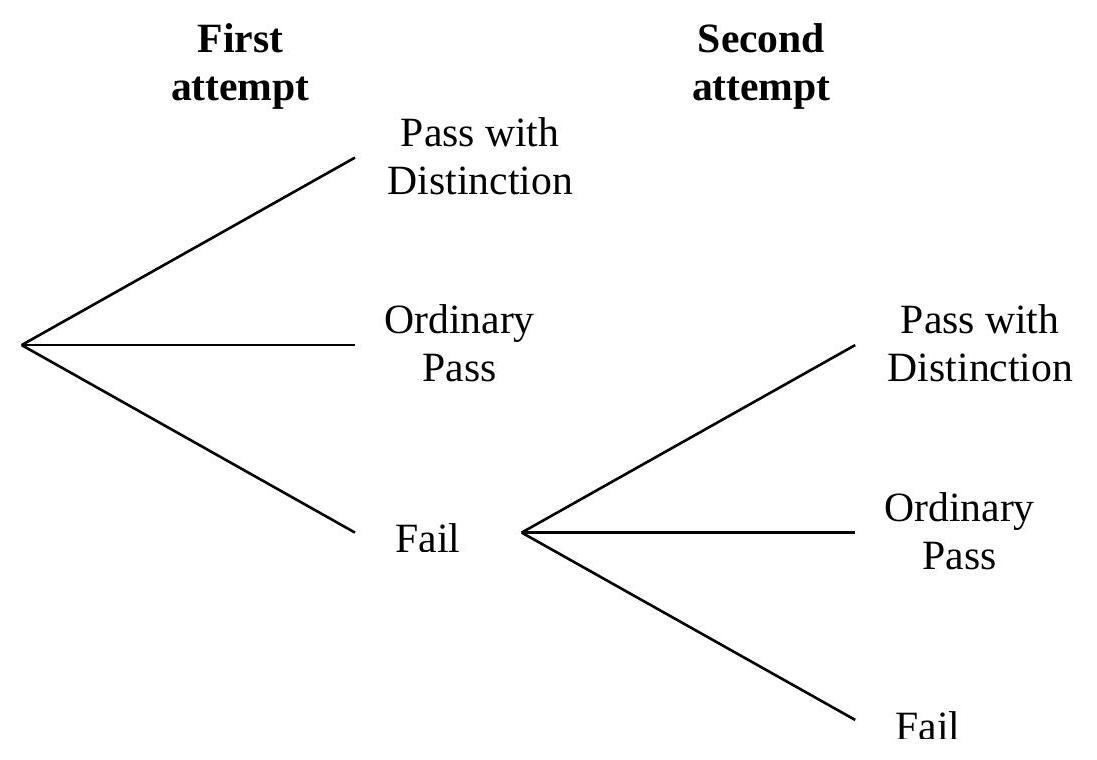
(a) Find the probability that, following a second attempt if needed, a randomly chosen candidate:
(i) fails the examination
(ii) passes the examination (with or without distinction)
(b) Jill and Jo are two randomly chosen entrants for the examination. Find the probabilities that
(i) both pass (with or without distinction), but just one of them needs a second attempt,
(ii) Jill gets a better result than Jo.

(a) Find the probability that, following a second attempt if needed, a randomly chosen candidate:
(i) fails the examination
(ii) passes the examination (with or without distinction)
(b) Jill and Jo are two randomly chosen entrants for the examination. Find the probabilities that
(i) both pass (with or without distinction), but just one of them needs a second attempt,
(ii) Jill gets a better result than Jo.
