Trigonometric Identities

1. Solve the equation for .
2. In this question you must show detailed reasoning

The curves and , meet at the point P , as shown below.

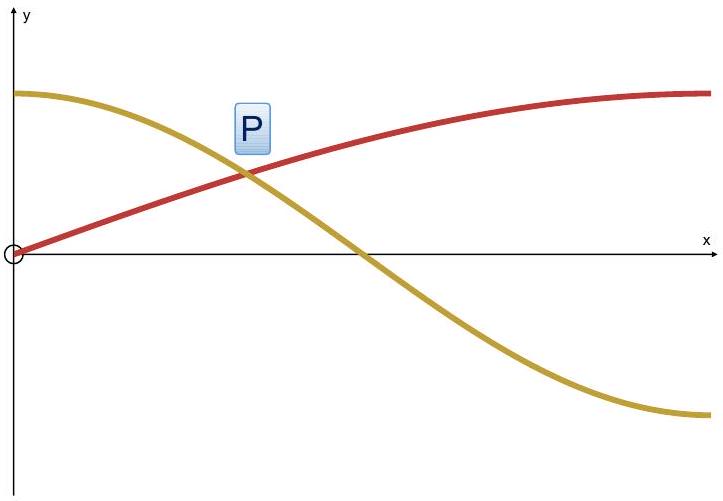
Find the coordinates of the point P .
3. Prove that .
4. (a) Describe a sequence of three transformations that maps the graph of on to the graph of , where is measured in radians, justifying your answer fully.
(b) Find the range of the function
5. (a) Prove that
(b) Solve the equation for .
6. When a bicycle is travelling at a constant speed, the height above the ground of the valve on the tyre measured in metres at time seconds, can be modelled by the function:

where angles are measured in radians.
Showing your working carefully, find:
(a) The maximum height of the valve above the ground, in metres to 2 significant figures, and the first time that this occurs, in seconds to 2 significant figures.
(b) The distance of the valve from the outer circumference of the tyre, in metres to 1 significant figure.
The time taken for the tyre to complete one full revolution, in seconds to 2 significant figures.
(d) The speed of the bicycle, in metres per second to 2 significant figures.