Numerical Methods

mpx

drawing

(a) By considering turning points, show that has only one real root and that this root lies between -2 and -1

Hint

Find the cubic function values at -2 and -1, and identify the “change of sign”, that means at least one root in that interval.
Differentiate the cubic to find its turning points. Then find second derivative to classify the turning points as local maxima or minima. If both local minima and maxima are above or below the x-axis, then there is only one real root between -2 and -1.

Solutions

Let

Since

is continuous and changes sign on

, the Intermediate Value Theorem guarantees at least one root in the interval

.

Then do first derivative to find turning points:

so the turning points are

and

.

Now calculate the second derivative to find the nature of these turning points (maxima or minima):

hence

(a local maximum at

) and

(a local minimum at

).

Evaluate

at these points:

Since both the local maximum and local minimum lie above the

-axis, the cubic changes sign exactly once as it goes from

to

. Therefore

has exactly one real root.

Hence the equation

has exactly one real root, and that root lies between

and

.

(b) Show that this root is -1.104 , correct to 3 d.p.

Hint

Since the question says the root is -1.104 and asks for 3 decimal places, we can try -1.1045 and -1.1035 to see which side of the root they are on. Then we can keep halving the interval until we reach the desired accuracy.

Solutions

I would try with

and

. So the root is between -1.1045 and -1.1035.
Since it asks for 3 decimal places, we can stop here and say the root is

, when round any values inside this range to 3 decimal places, it would be

. Isn’t it?

(a) Show that the equation has a real root between and .

Hint

Evaluate the function at the endpoints of the interval and check for a sign change.

Solutions

Consider the function

The function

is continuous for all real

. Evaluate

at the endpoints of the interval

:

Since

is continuous on

and

have opposite signs, the Intermediate Value Theorem guarantees the existence of at least one

with

Hence there is a real root of

in the interval

.

(b) Use the iterative formula

, starting from

, to find two further approximations to the root.

Hint

Use “fixed point iteration” method. Start with the initial guess

, then compute

and

using the given iterative formula.

Solutions

Two iterations of the map

starting at

Given

and

, compute

and

.

First iteration:

Second iteration (use the value of

above):

Therefore the two further approximations are

Show that the root is 2.081 correct to 3 decimal places.

Hint

Can try same method as in question 1(b), use “sign of change” method to verify the root is between two values that round to 2.081 when rounded to 3 decimal places.
These two values can be 2.0805 and 2.0815.

Solutions

Consider the fixed-point iteration

Check if it is correct to 3 decimal places by using “sign of change” method:
Using

and

Since there is a sign change between

and

, the root lies between these two values. Therefore, the root is approximately

(a) Show that the gradient of is always positive and deduce that the equation has one real root only.

Hint

If the derivative (gradient) is always positive, then the function is strictly increasing for all values of x
A strictly increasing continuous function can have at most one real root. Then just need to show a root exists by using “change of sign” method.
When using change of sign method, try evaluating at some special points, like

.

Solutions

Consider the function

Differentiate with respect to

:

Since

for all real

, we have

so

for every real

. Hence the function is strictly increasing on

.

A strictly increasing continuous function can have at most one real root. To show a root exists, evaluate at two points:

By the Intermediate Value Theorem there is some

with

. Combining existence with uniqueness we conclude that the equation

has exactly one real root (located in the interval

).

(b) Show that this root lies between

and

.

Hint

sometimes the hint is on the question itself 😃 This question b is hint for question a when doing “sign of change”.

Solutions

Let

. Evaluate at the endpoints

and

:

Since

is a polynomial, it is continuous on

. By the Intermediate Value Theorem (change of sign) there exists some

.

Show that the equation can be rearranged into the form

.

Hint

Start from the equation

Solutions

Start from the equation

Bring the constant to the right-hand side:

Factor out

on the left:

Divide both sides by

. Note that

for all real

, so this division is valid, thus the equation can be written in the fixed-point form:

(d) Using the iterative formula

and starting from

, find the next two approximations

and

to the root.

Hint

Using the formula from question ©, substitute

to find

, then substitute

to find

.

Solutions

Using the iteration

and starting with

, we compute:

(e) The diagram below shows part of the graphs of

and

, and the position of

.

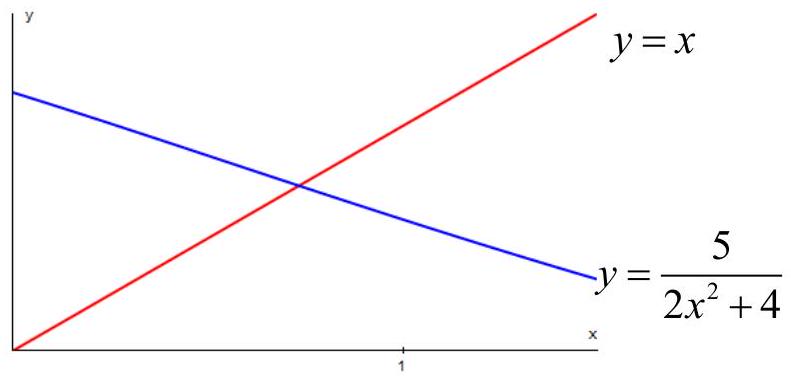
Copy the diagram and draw on it a staircase or cobweb diagram to illustrate how the iterations converge to the root. Indicate the positions of

and

on the

-axis.

Hint

Draw the CobWeb diagram step by step:

Start at the point on the x-axis.
Then draw and using the iterative formula.

Solutions

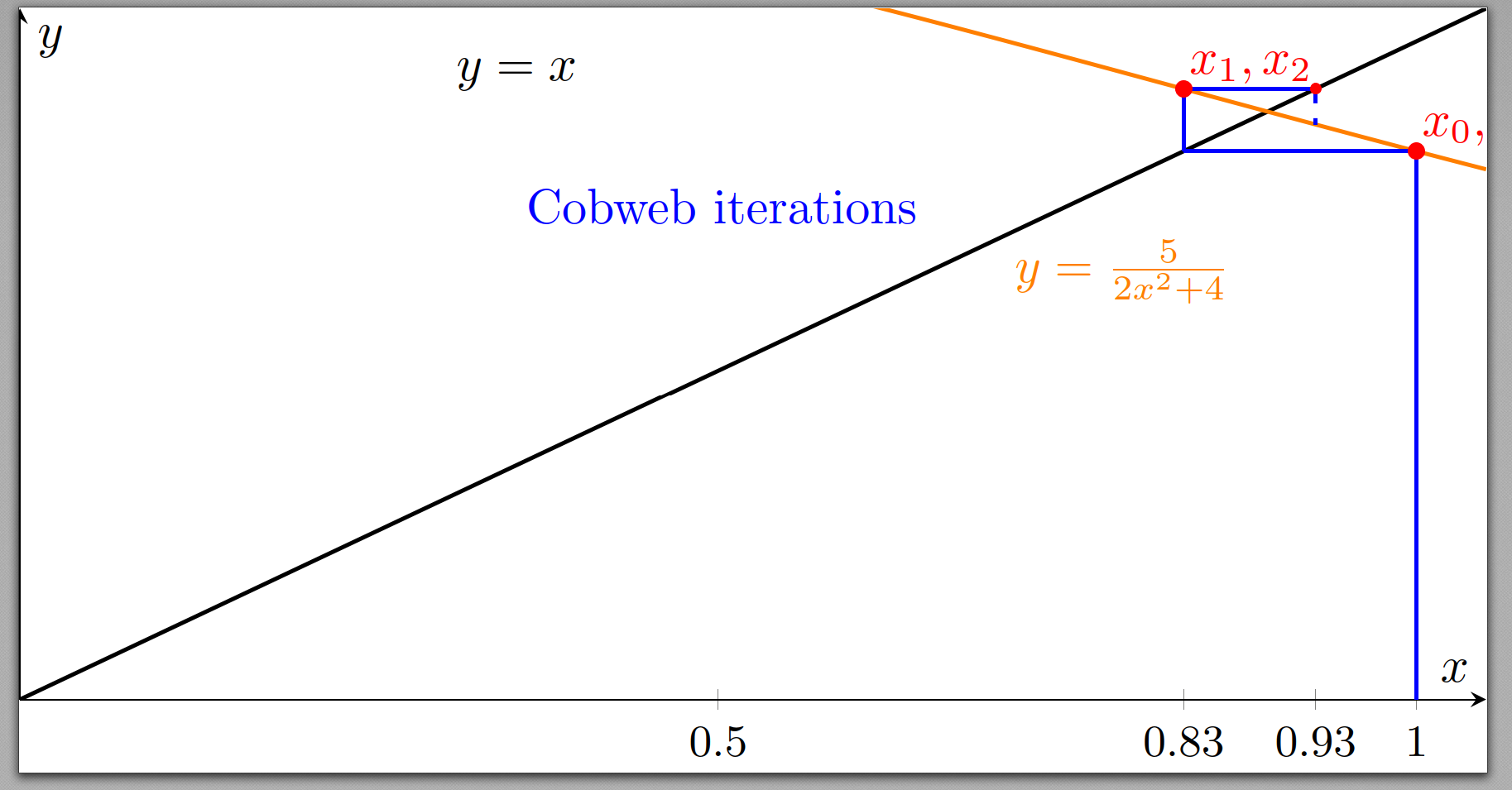
drawing

(f) Show that the root is 0.893 correct to 3 decimal places.

Hint

Same as previous “sign of change” method, try evaluating at two values that round to 0.893 when rounded to 3 decimal places, e.g. 0.8925 and 0.8935.

Solutions

Consider the function

. Evaluate at two points:

Since there is a sign change between

and

, the root lies between these two values. Therefore, the root is approximately 0.893 correct to 3 decimal places.

A sector AOB of a circle with radius 10 cm and centre O has an angle AOB of radians.
The chord AB divides the sector into two regions of equal area.

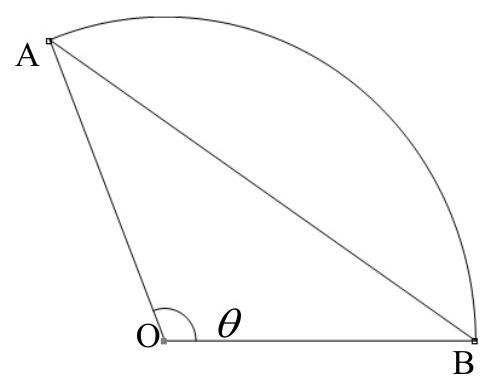
(a) Show that satisfies the equation .

Hint

The area of the sector AOB is given by

. The area of triangle AOB can be calculated using the formula

. Set the area of the triangle equal to half the area of the sector and simplify to derive the equation.

Solutions

The area of sector AOB is given by

The area of triangle AOB can be calculated using the formula

Since the chord AB divides the sector into two regions of equal area, we have

Substituting the expressions for the areas, we get

Simplifying this equation gives

Rearranging, we obtain the required equation:

(b) Use 3 iterations of the Newton-Raphson method, starting from

, to find the value of

correct to 4 decimal places.

Hint

calculate the derivative of the function

, then apply the Newton-Raphson iteration formula:

Perform 3 iterations starting from

.

Solutions

We want to solve the equation

using the Newton-Raphson method. The derivative of

is given by

The Newton-Raphson iteration formula is given by

Starting with an initial guess of

, we perform the iterations as follows:
1st iteration:

2nd iteration:

3rd iteration:

After 3 iterations, we find that

correct to 4 decimal places.

The diagram shows a cross-section of a tunnel. The height is measured in metres every 0.5 metres along the cross section.

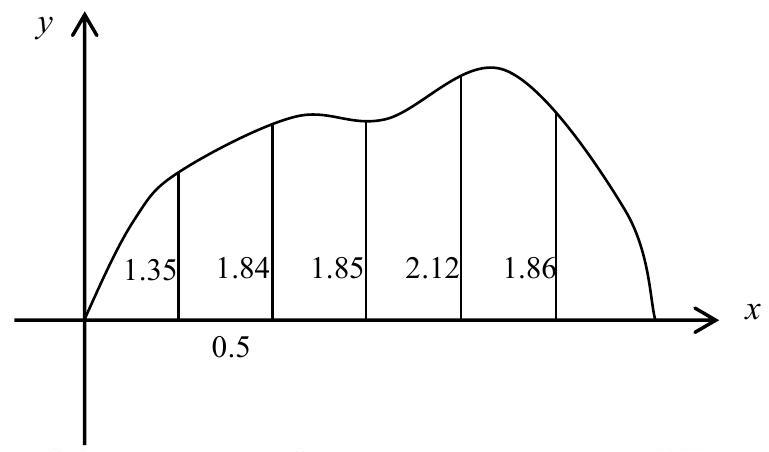
(a) Use the trapezium rule to estimate the area of the cross-section.

Hint

The trapezium rule formula is given by:

where

is the width of each interval and

are the heights at each measurement point. Here,

metres and the heights are given at intervals of 0.5 metres.

Solutions

Using the trapezium rule, we can estimate the area of the cross-section of the tunnel. The heights at each measurement point are as follows:

The width of each interval is

metres. The trapezium rule formula is given by:

Substituting the values, we get:

Calculating the sum inside the parentheses:

Now substituting back into the area formula:

(b) Is it an under-estimate or over-estimate?

Hint

Check if the curve has points of inflection. If it is always concave up, the trapezium rule gives an underestimate; if always concave down, it gives an overestimate. But if there are points of inflection, we cannot usually tell.

Solutions

Since there is a point of inflection in the curve, the curve changes between concave up and concave down, we cannot usually tell if it is an over-estimate or under-estimate just by looking at the graph.

An estimate is required for the integral .

Using 5 rectangles, find overestimates and underestimates for the value of the integral.

Hint

Firstly, decide whether the function \(f(x) = x \sqrt{x^3 + 1}\) is increasing or decreasing on the interval \([0, 1]\). Then, for the overestimate using right endpoints, divide the interval into 5 equal subintervals and calculate the function values at the right endpoints. For the underestimate using left endpoints, use the left endpoints of the same subintervals.

Solutions

The function

is increasing on the interval

.
To find the overestimate using right endpoints, we divide the interval

into 5 equal subintervals of width

. The right endpoints are

,

, and

.
Calculating the function values at these points:

The overestimate is given by:

To find the underestimate using left endpoints, we use the left endpoints

,

, and

.
Calculating the function values at these points:

The underestimate is given by:

drawing