Quadratic Functions

1. Find the set of values of , where , for which the equation has two distinct roots.

 Solutions

For two distinct roots, .

2. The graph shows the curve .
   
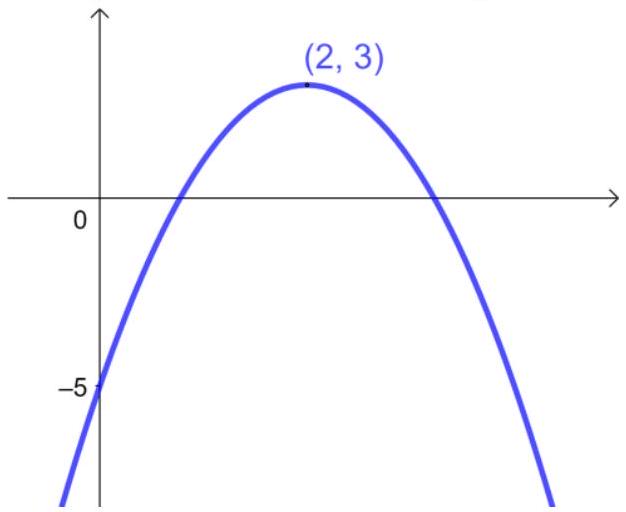
   Find the values of and .

 Hint

Use the completed square form of a quadratic, and use the turn point and y-intercept to find all parameters.

 Solutions

The turning point is at , so the completed square form is:

The y-intercept is at , so substituting these values in gives:

Substituting back into the completed square form gives:

So, , and .

3. The quadratic equation has equal roots.
   (a) Find the value of .

 Solutions

For equal roots, the discriminant .

(b) Solve the equation .

 Solutions

Substituting into the equation gives:

4. In this question you must show detailed reasoning.
   Show that the equation has no real roots.

 Solutions

Rearranging the equation gives:

Calculating the discriminant:

Since , the equation has no real roots.

5. Solve these equations, giving your answers in exact form.
   (a)

 Solutions

Let . Then the equation becomes:

Substituting back for gives:

(b)

 Solutions

Let . Then the equation becomes:

Substituting back for gives:

6. (a) Express in the form .

 Solutions

(b) The curve has a minimum point at .
Find the values of and .

 Solutions

Use the form obtained in question a and the turning point to find and .

We have:

At the minimum point, and . Substituting these values in gives:

solve above:

7. The diagram shows a right-angled triangle. Find the value of , correct to 3 s.f.

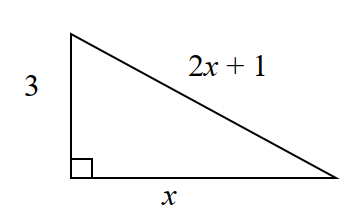
 Solutions

Using Pythagoras’ theorem:

Using the quadratic formula:

Since must be positive:

8. Amy throws a ball so that when it is at its highest point, it passes through the centre of a hoop. The path of the ball is modelled by the equation , where is the height of the ball in metres above the ground and is the horizontal distance in metres from the point at which the ball was thrown. The centre of the hoop is at the point where and .
   (a) Find the values of and .

 Hint

Use the completed square form of a quadratic and turning point to find and then substitute to find .
The turning point is at .

 Solutions

Use the completed square form to find since the highest point is at .

So, and .

(b) Find the value of at which the ball hits the ground.

 Hint

When the ball hits the ground, . Set and solve for .

 Solutions

To find when the ball hits the ground, set and solve for :

Using the quadratic formula:

Since must be positive: