Moments of Forces

- A rectangular lamina ABCD lies on a smooth surfance. The sides AB and AD measure 1.7 m and 1.4 m respectively. Horizontal forces of
and 25 N act at and the midpoint of BC at right angles to the edges as shown in the diagram.
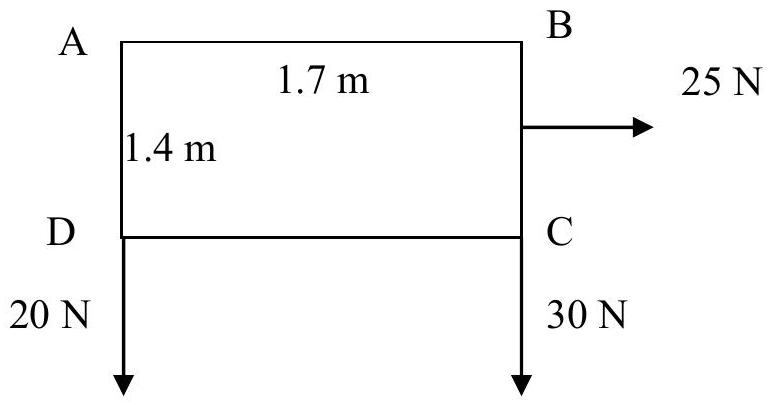
Calculate the total moment of the three forces about A .
Solutions
The moment of the
The moment of the
The moment of the
The total moment about A is
The moment of the
The moment of the
The total moment about A is
- Matt is trying to keep a freely hinged door closed while Jill and Wini are on the other side trying to push it open. The door is 60 cm wide.
Matt can exert a maximum force of 225 N . Jill and Wini exert forces of 200 N and 150 N atto the door.
Jill exerts her force 10 cm from the edge of the door, and Wini in the middle as shown in the diagram.
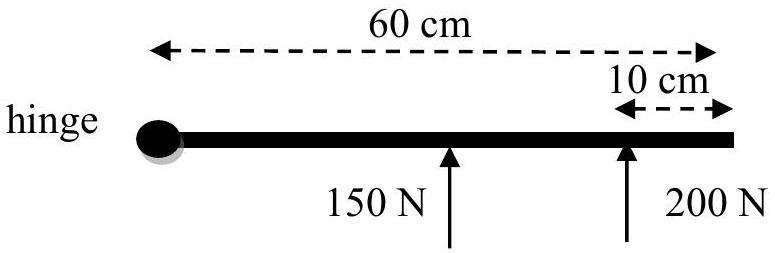
Determine whether Matt can keep the door closed.
Hint
To maximise his moment, Matt should push at the edge of the door opposite to the hinges.
Careful that the unit of length need to be consistent and better convert it to metres when calculating moments in Nm.
Careful that the unit of length need to be consistent and better convert it to metres when calculating moments in Nm.
Solutions
The moment of Jill’s force about the hinges is
The moment of Wini’s force about the hinges is
The total moment about the hinges is
The moment of Matt’s force about the hinges is
Matt cannot keep the door closed as
The moment of Wini’s force about the hinges is
The total moment about the hinges is
The moment of Matt’s force about the hinges is
Matt cannot keep the door closed as

A uniform rod AB of length 8 m and weight 180 N is held in horizontal equilibrium by two vertical wires. One wire is 1 m from A and the other 2 m from B .
(a) Draw a diagram showing all the forces acting on the rod.
(a) Draw a diagram showing all the forces acting on the rod.
Solutions
The forces acting on the rod are:
- The weight of the rod (180 N) acting vertically downwards at the centre of mass, which is 4 m from A .
- The tension in the wire 1 m from A , acting vertically upwards.
- The tension in the wire 2 m from B , acting vertically upwards.
(b) Calculate the tensions in the wires.
Hint
Can use different points to take moments about. Use centre of the rod, or use Point A, or Point B.
Remember to set up equations for vertical equilibrium as well.
Remember to set up equations for vertical equilibrium as well.
Solutions
Let the tension in the wire 1 m from A be
Taking moments about A :
Taking moments about A :
Also, since the rod is in vertical equilibrium:
From (2), we have
Substituting into (1):
Substituting into (1):
Substituting back into (2):
=========
If use moments about center of rod:
Taking moments about the center of the rod:
If use moments about center of rod:
Taking moments about the center of the rod:
Also, since the rod is in vertical equilibrium:
From (3), we have
Substituting into (2):
Substituting into (2):
Substituting back into (3):
- An injured climber is tied to a stretcher AB of length 2.5 m . The total mass of the climber and the stretcher is 90 kg.
In this question you should make the following modelling assumptions:
- the centre of mass, G , of the stretcher with climber is a distance 1.875 m from the end A of the stretcher, as shown in the diagram,
- all the forces acting on the system are in the same vertical plane.
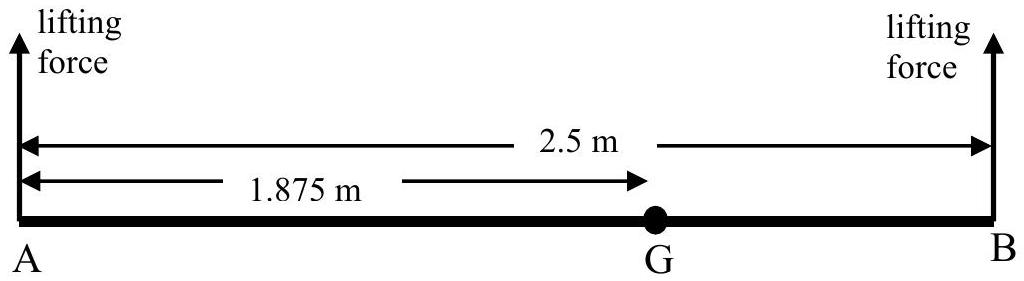
The lifting forces are each vertically upwards at the ends A and B of the stretcher, and the stretcher is held in horizontal equilibrium, as shown in the diagram above. Calculate the values of the lifting forces.
Hint
Let the lifting force at A be
The weight of the stretcher and climber is
Can use Point A or Point B to take moments about.
The weight of the stretcher and climber is
Can use Point A or Point B to take moments about.
Solutions
Let the lifting force at A be
The weight of the stretcher and climber is
Taking moments about A :
The weight of the stretcher and climber is
Taking moments about A :
Also, since the stretcher is in vertical equilibrium:
Substituting the value of
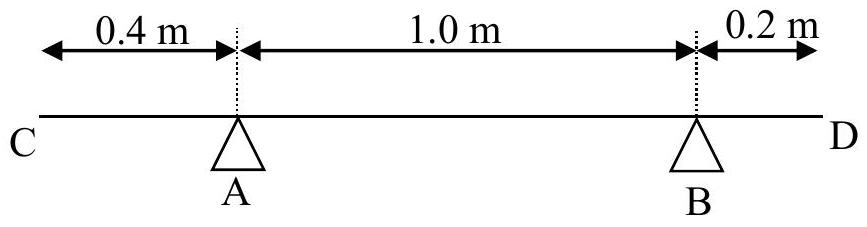
A uniform, horizontal, rigid shelf CD has a weight of 40 N and length 1.6 m . It is resting on two thin brackets A and B which are 0.4 m and 0.2 m respectively from C and D , as shown in the diagram above.
(a) Calculate the reaction forces of the brackets on the shelf.
(a) Calculate the reaction forces of the brackets on the shelf.
Hint
Just use the principle of moments and vertical equilibrium.
Reaction forces at A and B are upwards, and is equal to the weight of the shelf downwards.
Reaction forces at A and B are upwards, and is equal to the weight of the shelf downwards.
Solutions
Let the reaction force at A be
Taking moments about C :
Taking moments about C :
Also, since the shelf is in vertical equilibrium:
From (2), we have
Substituting into (1):
Substituting into (1):
Substituting back into (2):
An object is placed on the shelf so that its weight,
(b) Show that the vertical reaction force on the shelf at A is
(b) Show that the vertical reaction force on the shelf at A is
Hint
Similar to part (a), but now there is an additional weight W acting downwards at a distance x from C.
Solutions
Let the reaction force at A be
Taking moments about C :
Taking moments about C :
Also, since the shelf is in vertical equilibrium:
From (2), we have
Substituting into (1):
Substituting into (1):
Substituting back into (2):
Hint
Now need to use Point A as the pivot point to take moments about.
And remember, when the shelf is just about to tip, the reaction force at B is zero, so we just need to consider the moments from weight of shelf and the object.
And remember, when the shelf is just about to tip, the reaction force at B is zero, so we just need to consider the moments from weight of shelf and the object.
Solutions
Taking moments about A when the shelf is just about to tip:
