Forces and Newton's Laws

Use unless stated otherwise.

1. A particle is moving with constant velocity. Three forces and act on the particle, where and . Find the values of and .

 Hint

Since it is moving with constant velocity, the net force is zero. Therefore, the sum of the forces must equal zero.

 Solutions

The forces are

For constant velocity the net force is zero, so

Equating components gives

Solving these,

Therefore and .

2. (a) Calculate the acceleration of an object of mass 150 kg subject to a net force of 60 N .

 Hint

Use Newton’s second law, which states that the acceleration of an object is given by the net force acting on it divided by its mass :

 Solutions

Using Newton's second law,

With and ,

Therefore the acceleration is .

(b) A load of mass 150 kg is accelerating vertically upwards as the result of the pull of a crane wire. The tension in the wire is 1488 N .
Assuming that the only forces acting on the load are its weight and the tension in the wire, calculate the acceleration of the load.

 Hint

Calculate the weight of the load first, then find the net force acting on the load. Finally, use Newton’s second law to find the acceleration.

 Solutions

Given a load of mass and tension . Take .

The weight is

The net upward force is

By Newton’s second law, the acceleration is

Therefore the acceleration of the load is upwards.

3. A car of mass 1500 kg is pulling a trailer of mass 900 kg along a straight, horizontal road. The coupling between the car and the trailer is light, rigid and horizontal.

The motion of the car and trailer is modelled assuming that the resistances to motion are negligible. There is a driving force of 600 N acting on the car.
(a) Draw separate diagrams showing the horizontal force(s) acting on
(i) the car.

 Solutions

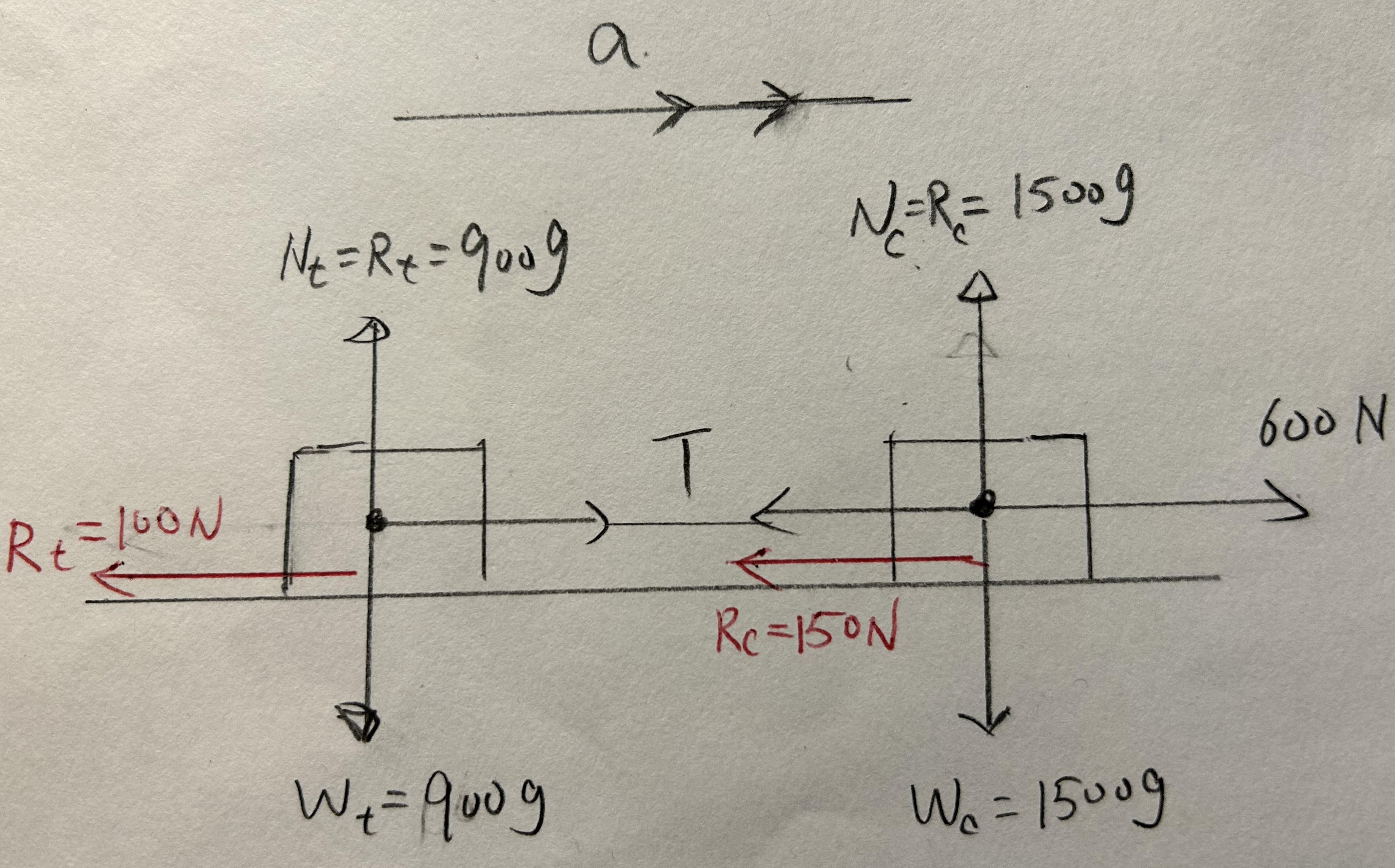
(ii) the trailer.

 Solutions

(b) Calculate the acceleration of the car and trailer.

 Hint

Use Newton’s second law to find the acceleration of the combined mass of the car and trailer.

 Solutions

Apply the Newton’s second law to the whole system of car and trailer.

The total mass of the car and trailer is

The driving force is

Using Newton’s second law, the acceleration is

Therefore the acceleration of the car and trailer is .

The situation is remodelled to include a constant resistant force of 150 N on the car and 100 N on the trailer.
Find the tension in the coupling.

 Hint

Again, use Newton’s second law to find the acceleration of the combined mass of the car and trailer, taking into account the resistant forces. Then, use this acceleration to find the tension in the coupling by considering the forces acting on the trailer.

 Solutions

We can use Newton’s second law on whole system to find the acceleration first. Or we can focus on the forces acting on the car or trailer. Here we use the the trailer.

The total resistant force is

The net force acting on the car and trailer is

Using Newton’s second law, the acceleration is

The forces acting on the trailer are the tension in the coupling and the resistant force of 100 N. Using Newton’s second law for the trailer,

Substituting the known values,

Solving for ,

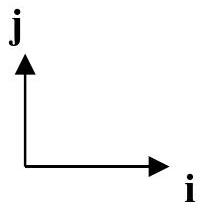
4. In this question, the unit vector is horizontal and the unit vector is vertically upwards. All forces are in Newtons.
   A small, heavy box is suspended in mid-air and is held in equilibrium by the tension in a light inextensible string and a horizontal force, as shown in the diagram.
   
   

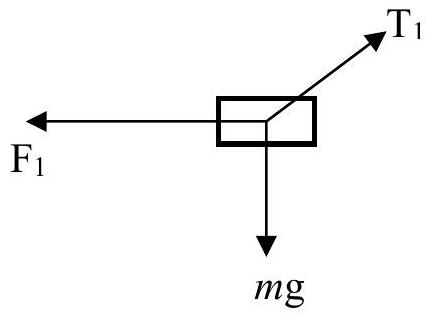
The tension in the string is , where . The horizontal force is , where .
(a) Find the value of .

 Hint

All forces acting on the box must sum to zero since it is in equilibrium. Therefore, the sum of the horizontal components of the forces must equal zero.

 Solutions

The forces acting on the box are the tension and the horizontal force . Since the box is in equilibrium, the sum of the forces must equal zero:

where is the weight of the box acting vertically downwards.
The horizontal components give:

Solving for gives:

Therefore, the value of is .

(b) Find the mass .

 Hint

The vertical components of the forces must also sum to zero. Use this to find the weight of the box, and then use the weight to find the mass.

 Solutions

The vertical components of the forces give:

where is the weight of the box. Solving for gives:

The weight is related to the mass by the equation:

where is the acceleration due to gravity, approximately . Solving for gives:

Calculate the magnitude of and the angle that makes with the horizontal.

 Hint

Use the Pythagorean theorem to find the magnitude of the tension vector. To find the angle, use the tangent function.

 Solutions

The magnitude of the tension vector is given by:

The angle that makes with the horizontal can be found using the tangent function:

Solving for gives:

Therefore, the magnitude of is approximately and the angle it makes with the horizontal is approximately .

Another force is now applied to the box. The force still acts and the box is still in equilibrium.
(d) The new tension in the string is . Calculate the values of and .

 Hint

Since the box is still in equilibrium, the sum of all forces acting on it must equal zero. Set up equations for the horizontal and vertical components of the forces and solve for and .

 Solutions

The forces acting on the box are now the tension , the horizontal force , and the new force . Since the box is in equilibrium, the sum of the forces must equal zero:

where is the weight of the box acting vertically downwards.
The horizontal components give:

Solving for gives:

The vertical components give:

Solving for gives:

Therefore, the values of and are and , respectively.

5. A girl of mass 48 kg takes a lift from the ground floor up to the second floor. She is holding a package that weighs 5 kg by means of a light inextensible string.
   The lift initially accelerates at and then travels at a constant speed of . Finally, the lift decelerates at .
   The normal reaction of the floor of the lift on the girl is .
   (a) Find the minimum value of during the motion.

 Hint

Consider the different phases of the lift's motion: acceleration, constant speed, and deceleration. The minimum value of $R$ will occur during the deceleration phase. Use Newton's second law to find $R$ during this phase. Thw

 Solutions

Calculate the normal reaction during each phase of the lift’s motion. The total weight will be :

1. During acceleration ( ):
   
2. During constant speed ( ):
   
3. During deceleration ( ):
   

The minimum value of occurs during the deceleration phase, which is .

(b) Given that the string does not break during the motion, find the maximum tension in the string during the motion.

 Hint

The maximum tension in the string will occur during the acceleration phase of the lift’s motion. Use Newton’s second law to find the tension during this phase.
Similarly, calculate the tension during constant speed and deceleration phases to confirm the maximum value.

 Solutions

Calculate the tension in the string during each phase of the lift’s motion.

1. During acceleration ( ):
   
   2. During constant speed ( ):
   
   3. During deceleration ( ):
   
   The maximum tension in the string occurs during the acceleration phase, which is .

6. Three particles, and C , are attached by light inextensible strings AB and BC . Particles A and B are held at an equal height of 2 m above a horizontal floor. B rests on a rough horizontal surface and when in motion experiences a constant resistive force of N. The string passes over two smooth pulleys.
   

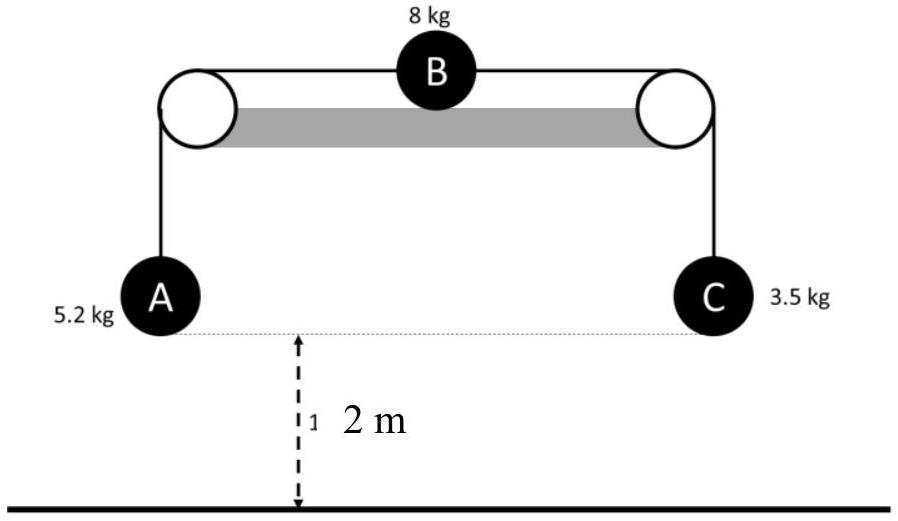
The masses of the particles are and 3.5 kg respectively.
It is given that B does not reach either pulley during any part of the motion following release.
The particles are released and A hits the ground 4 seconds later.
(a) Find the tension in each of the strings AB and BC .

 Hint

To find the tension in the strings AB and BC, we first need to determine the acceleration of the system. Since particle A hits the ground after 4 seconds, we can use the kinematic equation to find the acceleration.

Consider the acceleration on the whole system and then analyze the forces acting on each particle to find the tensions in the strings.

 Solutions

To find the tension in the strings AB and BC, we first need to determine the acceleration of the system. Since particle A hits the ground after 4 seconds, we can use the kinematic equation to find the acceleration.
The distance fallen by particle A is given by:

where , , and . Substituting these values gives:

Now, we can analyze the forces acting on each particle to find the tensions in the strings.
For tennsion on string AB:

Fpr tension on string BC:

(b) Find the exact value of .

 Hint

To find the value of , we need to analyze the forces acting on particle B. The tension in string AB and the tension in string BC will help us set up an equation involving . Use Newton’s second law to relate these forces and solve for .

 Solutions

To find the value of , we need to analyze the forces acting on particle B. The tension in string AB and the tension in string BC will help us set up an equation involving .
Using Newton’s second law for particle B:

Explain how you have used the modelling assumption that the pulleys are smooth.

 Solutions

The assumption that the pulleys are smooth implies that there is no friction between the string and the pulleys, allowing us to analyze the forces acting on each particle without considering any additional forces due to friction at the pulleys.

The particle A detaches from the string as soon as it hits the floor.
(d) Find the acceleration of the system when C is moving downwards.

 Hint

Basically we can treat the question as new system with only particles B and C.
The friction force still acts on particle B, but with different direction.

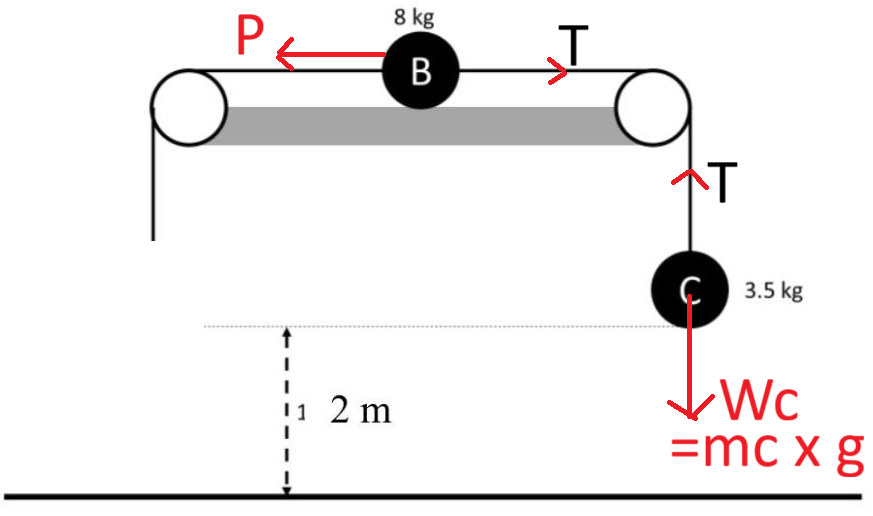
 Solutions

Let the acceleration after A detaches (with C moving downwards taken as positive) be .
Consider the whole system of particles B and C, the only forces acting on the system are weight of C and friction P toward left, so we have:

so

Using the exact values , , and we have

and

Therefore